참고문헌
- The Birth of Topological Insulator (Joel E. Moore, 2010)
- 스핀류와 위상학적 절연체
- Weak localization and weak anti-localization in topological insulators, Hai-Zhou Lu and Shun_Qing Shen
- Spin-Orbit Torques and Galvanomagnetic Effects Generated by the 3D Topological Insulator HgTe
- R. Winkler, Spin-Orbit Coupling Effects in Two-Dimensional Electron and Hole Systems.
Springer Berlin Heidelberg, 2003. - J. Chu and A. Sher, Physics and Properties of Narrow Gap Semiconductors. Springer, 2008
- A. Pfeuffer-Jeschke, Bandstruktur und Landau-Niveaus quecksilberhaltiger II-VI Heterostrukturen.
PhD thesis, Universität Würzburg, 2000. - Gauge Fields in Spintronics
0. Intro
Topological insulator는, 일반적인 부도체와 다르게 표면에 메탈과 같은 상태(states)를 갖는다. 이 상태들은 위상학적 효과에 의해 만들어지는데, 이 효과가 존재할 시 전자들은 부도체의 표면을 불순물 산란에 영향을 받지 않은채로 이동할 수 있다. 이를 Topological protection이라 하며, 이는 물질의 구조적 특성에서 오는 것이 아니라 추상적인 topological structure로 부터 기인한다. This structure can be characterized by a topological invariant, which is a mathematical quantity that remains unchanged even when the system is subject to small perturbations. 위상부도체는 새로운 상(phase) 또는 particle의 탄생을 이끌어 낼 수 있을 뿐만 아니라, 더 나아가 양자컴퓨팅, 스핀트로닉스등 최첨단 분야에 응용될 수 있을 것이다.
1. Vector Potential
시스템 내에 입자가 존재할 때, 입자에 작용하는 힘은 field로 볼 수 있다. 이때 field는 크게 발산장과 비발산장으로 나눌 수 있으며, 비발산장은 scalar potential(ex: 전기장-전위)을 정의할 수 있다. 반면에 비발산장은 scalar potential 정의가 불가능하며, vector potential을 정의하게 된다. 자기장과 vector potential사이의 관계식은 아래와 같이 나타낼 수 있다.

여기서 vector potential에 대한 식으로 구하기 위해서는, 자기장의 적분을 수반하게 되며 이때 자유도(적분상수) C가 만들어진다. 이는 다시 말하면 서로 다른 두개의 벡터포텐셜에 대해서 미분을 했을 때 같은 자기장이 나올 수 있다는 의미가 되며, 여기서 자유도가 임의의 scalar 함수의 gradient인 경우, 임의의 scalar 함수에 대해서도 성립한다는 것을 수학적으로 보일 수 있다.

물리적으로 정리하자면, 다양한 vector potential에 대해서도 우리가 관측하는 물리가 불변할 수 있다는 것이며, 이는 소위 말하는 gauge invariance이다.
특정 시스템에 따라 우리가 $\Lambda$의 gradient를 잘만 선택하면 문제를 이전보다 매우 쉽게 풀 수 있으며, 이를 gauge transformation이라 한다. 그리고 각각의 gauge는 이를 제안한 사람의 이름을 따 만들어졌다.
- Coulomb gauge
- Lorenz gauge
- Abelian gauge
- Weyl gauge
- Multipolar gauge
- Fock-Schwinger gauge
- Dirac gauge
2. Berry Phase
이 Vector potential과 Gauge invariance의 개념을 양자역학으로 갖고와보자. 양자역학에서 실제 우리가 관측할 수 있는 것과 우리가 관측하지는 못하지만 수식적으로 사용하는 대표적인 예가 바로 파동함수와 확률밀도 함수이다.
파동함수는 우리가 슈뢰딩거 방정식을 이용하여 system의 상태를 묘사하는데 사용하지만, 우리가 실제 관측하는 것은 이 파동함수의 제곱이 확률밀도이다. 앞에서 처럼 파동함수는 변화시키지만, 우리가 관측하는 확률은 변하지 않게하는 방법에는 무엇이 있을까? -> 대표적인 방법으로 파동함수에 위상을 곱하는 방법이 있다.
확률밀도함수는 파동함수의 절대값의 제곱이므로 켤레복소수 곱셈이 들어가며 이 과정에서 위상정보는 사라지게 된다.
즉, 양자역학에서의 게이지 변환은 위상의 자유도와 연관된다.
이처럼 위상이 더해져도, 우리가 구하는 확률이 갖기 위해서는 슈뢰딩거 방정식 역시 이전과 동일하게 풀려야 할 것이다.


위 식 양변에 bra vector $\langle \psi_n(\vec{x},t)|$을 곱하면

이제 위 식을 $\cfrac{\partial \Lambda}{\partial t}$에 대해 정리 후 시간에 대해 적분하면


위 식에서 우항의 첫번째 값은 시간에 의존하므로 dynamic phase, 두번째 값은 경로에 의존하므로 geometric phase라 한다. adiabatic을 가정하면 시간은 거의 무한대로 증가하지만 동시에 En의 변화가 없이 때문에 dynamic phase는 무시할 수 있다. 그렇기에 geometric phase만을 볼 때(경로만을 볼때), 이 경로가 만들 수 있는 수많은 경로 중, 우리가 관심 있는 것은 adiabatic 하게 폐곡선을 타는 경로이고, 이 때 geometric phase는 아래와 같다.

여기서 아래의 세개의 물리량을 정의한다.



갑자기 튀어나온 세 물리량에 당황할 수도 있지만, 이를 쉽게 이해하기 위한 두가지 방법이 존재한다.
2.1. Analogy of Magnetic Flux

Berry phase, Berry connection, 그리고 Berry curvature는 각각이 모두 전자기학에 나오는 물리량들과 비유적 설명이 가능하다. 수식적으로도 동일한 경향을 보이는데, 아래와 같이 나타낼 수 있다.

2.2. 굴렁쇠 비유
두번째 방법은 굴렁쇠 비유를 통한 예시이다. 사실 connection, phase, curvature는 모두 기하학에서 쓰이는 용어들이다.

굴렁쇠가 폐곡선을 따라 굴러가는 경우를 생각해보자. 굴렁쇠의 특정 점에 빨간 점을 붙여놓으면, 굴렁쇠를 한바퀴 굴렸을 경우 특수한 경우가 아니라면 이 빨간점이 시작점과 다른 위치에 있을 것이다.
이를 기하학적 phase mismatch라 하며, 이를 수식적으로 나타내기 위해 각 점에서의 빨간 점의 움직임을 담는 정보를 connection이라 한다. 각 점에서의 움직임이므로, 이 정보를 모두 모으면 위상의 변화가 된다.
그리고 phase mismatch가 같다고 한들 폐곡선이 형성하는 면적 넓이에 따라 곡률이 달라지며 여기서 곡률이 curvature이다.
3. Topology: Chern Number
3.1. Parallel Transport
Phase mismatch는 Intrinsic curvature 가 존재하는 공간에서는 임의적으로 나타날 수 있다. 일반적인 Euclidean plane에서 벡터를 평행이동 시키면 원래의 방향을 계속적으로 유지한다. 즉, 이런 세상에서는 phase mismatch가 애초에 존재하지 않는다. 하지만, 위 영상과 같이 curved surface에서는 이러한 평행이동이 존재하지 않는다. 대신, parallel transport라는 개념을 이용하며 이 때는 위의 영상 처럼 벡터가 움직인다.
Curved surface 위에서의 벡터는 본질적으로 자신의 상태를 유지한다 한들 위상의 변화가 발생하며, 우리가 양자역학에서 adiabatic approximation을 적용하여 closed loop을 한바퀴 도는 것은 curved surface에서의 parallel transport를 수행하는 것과 같다. (좀 다른 얘기지만 중력에 의해 곡률이 생기는 중력장을 생각해도 좋을 듯 하다)
3.2. Gauss-Bonnet theorem
지금까지의 이야기는 모두 geometry였다. 이를 topology와 연결시키기 위해서는 Gauss-Bonnet formula를 이용해야 한다.
아래 식에서 좌항은 우리가 앞에서 본 phase mismatch이며, 오른쪽의 topology의 g는 핸들의 갯수이다.

이 식은 설명하려면 또 시간이 많이 필요해서 아래와 처럼 털난 공 정리를 이용해서 설명하면, 어쨌든 중요한건 구멍의 유무에 따라 바꿀 수 없는 기하학적 특성이 무조건 존재한다는 의미이다. (추가 예정)
이를 물리적으로 갖고오면 앞에 Chern이라는 사람의 이름을 넣어 Chern-Gauss-Bonnet formula로 바뀌며, geometric항의 curvature는 Berry curvature로, topology항의 handle count는 Chern number로 바뀐다.

여기서 Chern number는 handle count와 같은 역할로 connection을 다양체 위에 올려 놓았을 때, 그 connection에 대한 위상론적인 정보를 담고 있는 값이다. handle count는 정의 자체가 핸들의 갯수이므로 정수이지만, Chern number는 과연 정수일까? 확인하기 위해 직접 적분을 해보자.

이때 적분하는 경로가 아래와 같다면,

폐곡선 경로적분은 아래와 같이 나타낼 수 있다.

이때 이 state가 adiabatic approximation이 적용된 상태에서 경로를 이동한다고 가정하면, 아래의 등식이 성립한다.

이 식을 위의 적분식에 대입하면,

위 식을 정리하면,

이제 다시 adiabatic approximation으로 가서 등식들을 조금씩만 가다듬으면

위 두 등식을 서로 나눠주면 아래와 같이 된다.
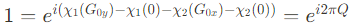
즉, adabatic approximation이 적용되는 한, Chern number Q는 integer값을 가지게 된다.
4. Integer Quantum Hall effect

Integer Quantum Hall Effect는 1980년 Klaus von Klitzing이 발견한 효과로서, 극저온에서 2DEG에 수직한 방향으로 매우 강력한 자기장을 인가(그러므로 TRS는 깨진다!)할 때, Hall conduntance가 양자화 되는 효과이다.
자석, 결정(crystals)처럼 질서(order) 상들은 대칭성붕괴(symmetry breaking)를 통해 그 성질을 묘사할 수 있다. 예를들어 결정 속 이온들은 정전기적 상호작용에 의해 주기적 정렬을 갖게 되는데, 이로 인해 공간 내에서 회전, 병진에 대한 연속 대칭성이 붕괴된다. 1980년대, 위와 같이 대칭성붕괴로는 상변화를 설명할 수 없는 경우를 발견하게 된다. 2차원에 속박되어있는 전자가 2차원 평면의 수직방향으로 강한 자기장을 받을 경우, 완전히 새로운 질서를 나타내게 되는데, 이는 기존의 대칭성붕괴로는 설명이 불가능하고, 위상학적으로 설명이 가능한 상태가 된다. 이를 양자 홀 효과라 한다.
이때 Hall conducatance 값은 condutance quantum $e^2/h$의 정수배이며, 이 처럼 자연에 존재하는 근본적인 상수에만 의존하고 샘플의 impurity, geometry, 그리고 전자밀도와는 관련이 없다. (In this case, topological invariant is Chern number) 이를 증명해보자.
Kubo formula 공식을 보면

이때 슈뢰딩거 방정식 $\hat{\mathcal{H}}|m\rangle=E_m|m\rangle$에 momentum derivative $\partial_{\vec{k}}$를 해주면,

여기서 양변에 bra vector $\langle n|$를 곱하면,

$n\ne m$을 이라하면, orthonormal basis가 기본 전제인 양자역학에서 $\langle n | m \rangle = 0$이 되고, 그리고 Hamiltonian의 momentum derivative는 아래와 같이 velocity operator 이므로,

다음과 같은 식이 도출된다.

위 식을 위에서 언급한 Kubo formula에 대입하면, 식은 아래와 같이 바뀐다.

여기서 Berry connection $A_m = i \langle m| \parital_{\vec{k}} m \rangle$을 가져오면, Berry curvature는 다음과 같이 수식적 전개가 가능하다.



여기서 identity operator $\mathbb{I}=\sum_n |n\rangle \langle n|$을 도입하면

위 식에서 다음의 성질을 이용하면, (+위 식에서 맨 오른쪽 항은, partial derivative가 commute 하므로 소거된다)

위의 Berry curvature 식은 아래와 같이 정리된다.

총 정리하면

즉, Hall conductance는 Chern number로 정의할 수 있으며, topological invariants 관점에서 설명할 수 있다. 이를 topology로 이해하기 위해서는, Fermi surface의 topology를 이해해야 한다.
일반적으로 1st BZ에서의 Fermi surface는 부도체, 금속에 따라 아래와 같은 형상을 가진다.

감을 챈 사람도 있겠지만, 부도체(Fermi sea가 BZ에 접하지 않아 완전한 구형태를 가짐), 도체(Fermi Sea가 BZ에 접하거나 이어져 구멍이 뚫림)를 나누는 좋은 기준이 바로 Fermi sea의 topology이다. Fermi sea가 BZ에 접한다는 것은, band structure 속 에너지 그래프가 $E_F$와 맞닿는다거나 아예 통과한다는 것이고, 이는 Fermi sea에 구멍을 만들어낸다. 이것이 conductivity를 바꾸는 요인이 된다.
수직으로 자기장이 강하게 작용하는 시스템 내에서는 Landau level이 정의되며 다음과 같이 Fermi sea가 slice된다.
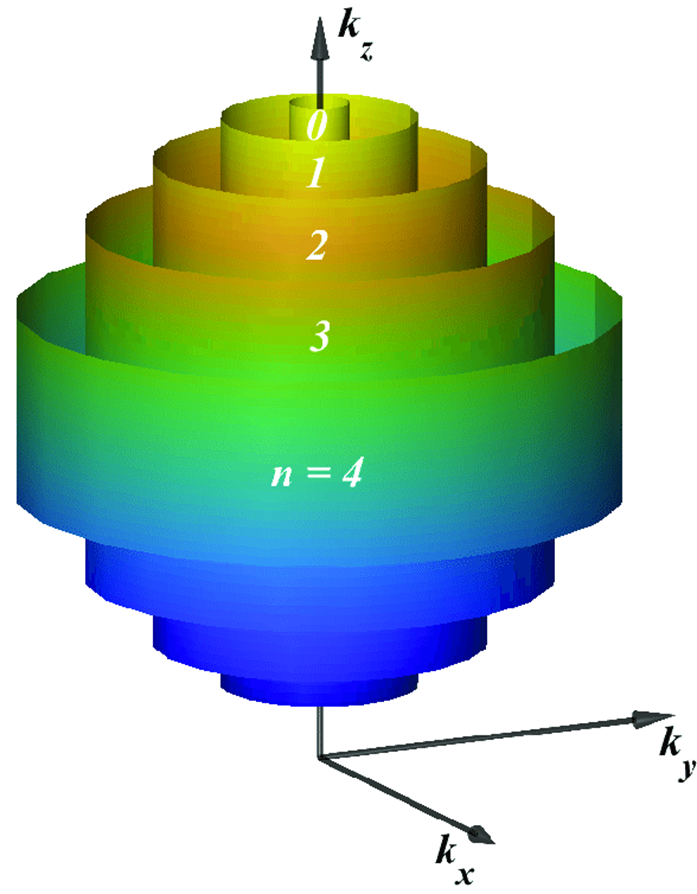
자기장이 강하게, 더욱 강하게 걸릴 수록 구의 slice 되는 정도가 커지며, 이 점이 Fermi sea의 topology를 변화시켜 conductance를 변화시키는 것이다. 마치 아래와 같이 그래프를 생각해도 좋다.

자기장이 커지면 커질수록 Potential 사이의 간격은 넓어지면서 자연스럽게 $E_F$를 거치게 된다. Landau level이 $E_F$를 거쳐가는 순간에 condcuctivity가 증가하면서 $R_xx$값이 0이 아닌 값을 가지고, Landau level을 지나친 이후에는 다시금 carrier가 없어져 insulator 형태를 가지게된다. 그리고 Edge states를 보면 Landau level이 지나감에 따라 $E_F$를 통과하는 그래프의 선 개수가 늘어나면서 topology가 바뀌어 Hall conductance가 변화한다고 이해하면 좋다.
소위 일반적인 글에서 Hamiltonian이 작은 deformation(perturbation)을 거치는 내에서는 Hall conductance가 불변하다는 관점은 위상학적으로 Fermi sea에서 구멍이 추가적으로 발생하지 않는다는 것이라고 볼 수 있다.
5. Quantum spin Hall effect
2005년, Kane과 Mele는 topology에 의해 보호되는 물질의 새로운 상태를 예측한다. 이는 그래핀 내에서 quantum spin Hall insulator state이다. 이 state는 두개의 서로 다른 방향으로 propagation하는 edge states로 구성 되며 이때 propagation 방향에 대해 서로 반대되는 스핀 방향을 갖는다(resembling the chiral edge modes in the IQHE, but with unconventional spin textures). 그리고 QH state와는 다르게, edge states를 만들기 위해 자기장을 필요로 하지 않는다. (SOC에 의한 것으로, 서로 반대방향으로 흐르는 전자들의 스핀 방향이 반대이므로 effective magnetic field 방향 역시 반대) 즉, TRS가 성립한다.
이러한 edge/surface state에서는 서로 다른 방향의 스핀이 서로 반대방향으로 흐르고, 이 성질을 helical이라고 부른다. 이 edge/surface 에는 평형 상태에서도 helical spin current가 항상 흐르고 있다. 평형상태에서는 그 스핀류를 외부로 빼낼 수 없지만, 샘플에 전기장을 가하게 되면, edge/surface spin current에 의하여, 인가한 전기장에 수직한 방향으로 스핀류가 흐르게 된다. 즉, spin Hall effect의 절연체 버젼이 Quantum spin Hall effect인 것이다.
하지만 실험적으로, 이러한 효과는 불가능한데, 이는 graphene을 구성하는 탄소가 매우 가벼운 물질이라 SOC가 작으므로, 효과를 관측하기 위한 energy scale역시 매우 작기 때문이다. Kane과 Mele의 연구 후에, Nernevig, Hughes, 그리고 Zhang은 이러한 state가 HgTe와 같은 다른 물질 시스템에서도 관측 될 수 있다고 예측해다. Hg와 Te는 모두 중금속으로, 강력한 SOC를 유발할 수 있으며 이를 통해 energy level에 대한 상대론적 correction이 유의미 해진다.
SOC와 HgTe의 무거운 질량의 조합은 이 물질 시스템의 band structure의 inversion을 야기한다(2.3.1에서 다룰 예정). 일반적인 trivial band structure에서, conduction band는 에너지적으로 valence band 위에 위에 위치해 있으며, 결과적으로 positive energy gap을 만들어낸다. 하지만 HgTe의 경우, 상대론적 correction이 non-trivial band structure를 야기하는데, 여기서 valence band가 에너지적으로 conduction band위에 위치하게 되며, 결과적으로 band structure가 반전된다.

이 energy iversion은 또한 system의 band topology의 변화를 암시한다. quantum confinement와 결합하여, HGTe quantum well은 topologically non-trivial state를 만들어내는데, 이것이 QSHE를 발현시킨다.

이 효과는 HgTe/(Hg,Cd)Te quantum well 구조에서 2007년에 처음 발견 됐으며, 이때 시스템의 conductance $G$는 $2e^2/h$의 값을 갖는다.
QSHE의 발견과 증명은 3D TI에 대한 예측을 만들어냈다. TI는 양자역학적 물질로 band gap 자체는 일반적인 부도체와 갖지만, topologically 보호되는 conducting surface를 갖게되는데 이것이 바로 band inversion에 의한 효과이다.

위와같이 Vacuum-Normal insulator로 이어지는 energy band 선을 보면 교차가 존재하지 않는다. 다시 말해 Fermi sea 부근에 carrier가 없다는 것이고 이는 우리가 알고있는 부도체이다. 하지만 TI에서는 band inversion으로 인해 TI-Vacuum 사이에 energy band를 이을 때 반드시 교차점이 존재하게 된다(우리는 이를 Dirac point라 한다). 이 교차점 부근에서 캐리어는 존재하게 되며 이는 TI와 vacuum 사이의 경계인 surface에서 발생하기에 일반적으로 우리는 이를 surface state라 한다.
이 surface state는 $k \sim 0 $(=Dirac cone)에서 linear dispersion을 가지며, Dirac point라 불리는 곳에서 서로를 관통한다. 이 states는 Dirac Hamiltonian을 통해 수학적으로 기술이 가능하다.

이 topological surface states는 band inversion에 의한 결과이므로, band structure가 크게 수정되는 경우(예를 들어 band inversion을 없애거나, insulating bulk gap을 닫는 등의) 없어질 수 있다. 또한 TRS에 의해 보호되기에, 비자성 impurity나 다른 TR invariant local perturbation은 elastic back scattering을 야기할 수 없다. 이로 인해 conductance는 매우 강력해진다.
Rashba ssytem과 유사하게, surface Hamiltonian의 TRS는 서로 반대 방향의 모멘텀($\vec{k}$, $-\vec{k}$)을 가지는 전자들에게 서로 반대되는 스핀을 부여한다. 하지만 이 때 발생하는 SML은 Rashba system에서의 SML과는 근본적으로 다른데, TSS는 band inversion에 의한 것으로 spin flipping 없이는 elastic backscattering이 억제되어, magnetic disorder에 대해서 states가 매우 튼튼하다는 것이다. 다음섹션에서는 HgTe를 예로 들어 band structure와 그 특성을 살펴보고자 한다.
6. The Mighty HgTe
이전 섹션에서, 우리는 SOC에 대해 소개하였으며, 이 물리적 효과가 TI의 존재에 있어 중요한 재료가 된다고 언급햇다. HgTe는 매우 특별하고 다재다능한 물질로서, 강력한 SOC를 가지면서 물질의 phase가 변한다.(Weyl semimetal에서 TI로 등등..) 이 섹션에서는 HgTe의 band structure에 집중하여, TI phase가 어떻게 얻어지는지 보고자 한다.
6.1. Band Inversion of HgTe
3D TI로서의 HgTe는 일반적으로 CdTe와 계면을 형성하므로, 이 섹션에서는 gTe와 CdTe를 묘사하는 Hamiltonain에 대한 relativistic correction을 소개할 것이며, 그들 각가이 서로 매우 다름을 보일 것이다. 이 corrections는 큰 원자번호를 가지는 원자들에 있어 매우 중요하며, 그러므로 HgTe와 CdTe의 band evolution을 이해하는데 결정적이다.
이전 섹션에서 언급했던 것 처럼, HgTe와 CdTe bulk material는 zinc blende lattice 구조를 가진다. 또한, II-VI compounds HgTe와 CdTe의 경우는 direct gap semiconductor(conduction band와 valence band의 극값은 모두 $\Gamma$ point (k=0)에 위치해있다). top valence band는 p-symmetric atomic orbital로 구성되며, six-fold degenerate인 반면에, conduction band는 s-states로 구성되고 two-fold degenerate(two spin states)이다.
이 bands들을 relativistic correction 없이 묘사하는 Hamiltoian을 $\hat{\mathcal{H}}_{nr}$이라 하자.
아래 Figs.2.4a와 2.4b에 나와있듯이, non-relativistic Hamiltonian $H_{nr}$에서 유도된 CdTe와 HgTe의 energy level은 서로 같다.

Non-relativistic Hamiltonian에 첫번째로 추가되는 correction은 Darwin term $H_D$이다. This correction smears the effective potential felt by the electron and changes its potential energy. 이 term은 orbial만을 포함한 경우에 적절하며 그러므로 두 화합물의 energy band alignment에 큰 영향을 끼치지 못한다.
하지만, mass-velocity correction ($H_{mv}$)를 고려하게 되면, HgTe의 band structrue가 CdTe에 비해 급격하게 달라진다. 이 correction은 conuction band와 valence band를 모두 낮은 에너지로 이동시키는데, 이는 Cd와 Hg의 원자 질량 차이 때문이다. 이 correction은 s-symmetric electron와 p-symmetric electron에 대해서 서로 다르게 작용하며, Fig. 6.1 과 같이 s electrons의 경우가 p electron의 경우보다 5배는 더 크게 나타난다. Hg의 atomic mass가 Cd의 atomic mass보다 더 크므로, 이 correction은 HgTe에 더 크게 작용하며, conduction band(s-states)를 CdTe의 것과 비교하여 더 큰 폭으로 낮춰버린다.
마침내, spin-orbit coupling tem이 valence band의 six-fold degeneracy를 $\Gamma_7$(two-fold degenerate)과 $\Gamma_8$(four-fold degenerate) bands로 분리시킨다. CdTe의 경우, 이 splitting은 positive energy band gap의 결과를 나타내지만, HgTe의 경우, $\Gamma_6$ band와 $\Gamma_8$ band의 inversion을 야기시켜 결과적으로 negative energy band gap ($E_G<0$)을 초래한다. 이 $\Gamma_6$ band와 $\Gamma_8$ band 사이의 inversion이 topological surface states를 얻기 위한 필요조건인 것이다.
The inversion between $\Gamma_6$ and $\Gamma_8$ bands is a necessary condition to obtain topological
surface states. The inversion happens between $\Gamma_6$ and all of $\Gamma_8$. The $\Gamma_{8,LH}$ are the relevant bands for the surface or edge states. It should, however, be reminded that unstrained bulk HgTe is a
semi-metal and that the topological insulator phase can only be achieved by opening the band
gap between the HH and LH bands that touch each other at the $\Gamma$ point.
In this case, the band structure of HgTe gives a key ingredient to engineer a topological insulator phase (band inversion)
3.2. Gap Opening in HgTe


3.3. Experimental Evidence for the Band Structure of HgTe
The main feature in this figure is the linear
dispersing band attributed to the surface states (SSB - originating from the inversion between the $\Gamma_{8,LH}$ and $\Gamma_{6}$ bands) coexisting with the bulk bands (BB - corresponding to the $\Gamma_{8,HH}$ band).
The Dirac point is assumed to be buried into the valence band, at approximately 30-50 meV below the band edge.
7. Topological Insulator
위상학적 절연체는 비자성 절연체의 새로운 양자성으로, bulk (샘플내부)의 에너지 분산에는 gap이 존재해서 비자성 절연체이지만, edge나 surface에는 gap이 존재하지 않아 금속과 같은 상황이 된다.
7.1. 2D Topological Insulator
TRS가 성립하는 계 중에서, "IQHE와 같은 성질을 가진 계는 없을까?" 라는 아이디어로 시작해 이론적으로 제안된 것이 바로 topological insulator이다. Up spin과 down spin 두 종류의 스핀을 가진 계를 생각하며, up spin은 Chern number Ch=1의 양자홀 계, down spin은 Chern number Ch=-1의 양자홀 계라고 하자. 이러한 상태는 up spin은 +z 방향의 자기장, down spin은 -z 방향의 자기장에 놓여있을 때 실현된다. (by SOC!!) 이러한 edge state는 up spin과 down spin이 같은 양. 반대 방향으로 흐르는 상태로서 pure spin current가 지속적으로 흐르는 상태라고 할 수 있다. Pure spin current는 TRS가 성립하므로, TI는 TRS가 성립한다.
7.1.2. Time Reversal Symmetry (TRS)
TRS는 시간의 흐름에 따라 기록한 비디오를 거꾸로 돌리는 조작과 같다. 이 변환에 의해 $t$는 $-t$로 manipulation 되고, 그에 동반한 물리량도 부호가 바뀐다.
대표적으로 Maxwell equation을 보면,

즉, Maxwell equation은 시간반전 조작에 대해 불변이라고 볼 수 있다.
양자역학에서 TR operator는 $\hat{\Theta}$라 하며, spinless 의 경우 $\hat{\Theta}$는 complex conjugate operator($\hat{K}$)와 같으므로, $\hat{\Theta} \psi = \psi^{*}$라고 표현도니다. 만약 spin 1/2인 경우에는, $\hat{\Theta} = i \sigma_{y} \hat{K} $로 쓸 수 있으므로,

만약 Hamiltonian $\hat{\mathcal{H}}$가 시간반전에 불변이라고 하면,

결정내부에서의 Hamiltonian은 위의 경우와 마찬가지로 격자만큼의 병진운동에 대해 불변이므로,

(* TR operator $\hat{\Theta}$ 은 anti-unitary operator로써 임의의 Hamiltonian $\hat{\mathcal{H}}$에 대해 다음이 성립한다! $\rightarrow$ $\hat{\Theta} \hat{\mathcal{H}} \hat{\Theta}^{-1} = \hat{\mathcal{H}}^{\dagger} $
이젠 TRS가 존재하는 시스템에서 Hamiltonian이 TRS라는 사실이 eigenstate에 어떤 영향을 끼치는지 보고자 한다. 일단 Schrodinger equation을 쓰면,

양변에 TR operator를 적용하면

위 식에서 알 수 있듯이 $\vec{k} \Leftrightarrow -\vec{k}$이 성립하므로, 에너지 밴드의 구조가 spatial inversion이 성립함을 알 수 있다.
여기에서 특별한 파수가 존재한다는 사실에 착안해보자. 그것은 바로 시간반전불변 운동량(time-reversal invariant momenta, TRIM)이다.
7.2. 3D Topological Insulator
그 다음의 이론적으로 중요한 발전은 2006년에 이루어졌다. 3D 상태에서 진짜로의 quantum Hall effect는 발생하지 않았지만, '약한' 3D 위상부도체가 만들어 질 수 있음을 알게됐다. 이는 2D 위상부도체를 겹겹이 쌓아 만드는 것으로, 결과적으로 disorder에 안정적이지않으며 그 물리는 2D state의 것과 유사하다.
• 2차원 위상학적 절연체 물질을 여러 겹으로 쌓아서 3차원으로 만든 것을 Weak Topological Insulator
• 원래부터 3차원적인 특징을 보여주는 물질을 Strong Topological Insulator
• 같은 속력으로 반대방향으로 움직이는 전자들이 설 ㅗ반대방향의 스핀을 가지고 있을때, 과학자들은 그 시스템은 시간역전 대칭성을 가진다고 말한다. -> 이론적으로 위상학적 절연체에서의 입자의 운동성은 시간 역전 대칭성에 의해 보호되는데, 한 방향으로 움직이는 입자는 같은 속력을 가지는 후방 산란을 하지 않는다는 말과 같다. 이렇게 후방 산란을 하지 않는 입자는 계속 앞으로 전진할 수밖에 없고, 이는 불순물에 의한 Anderson localization로부터 자유롭다.
자기장 없이 홀 전류의 변화를 억제하는 요인 : 절연체 표면에 존재하는 Karmer's doublet (크라머스 겹상태)와 그들이 보이는 Dirac Spectrum에서 기인.
시간 역전 대칭성이 유지도히는 한, 크라머스 겹상태가 나타나는 디락 스펙트럼에는 절대로 energy gap이 생길 수 없기 떄문에 위상 절연체의 표면은 항상 금속성을 띠게 된다.
위상 절연체 내부에는 가전자대와 전도대 사이에 놓인 벌크 에너지 간격 때문에 전류가 흐를 수 없으므로, 이러한 경우 외부 전압에 의해 가속되는 전자는 오로지 표면의 크라머스 겹상태를 따라 단열 수송 된다.
전자의 단열 수송 과정에는 에너지 손실이 없으므로 홀전도도는 일정한 상수값 1/2R_K 를 갖게 되는데, 이때 특이한 점은, 홀 전도도가 1/R_K 의 정수배가 아닌 그 절반의 값으로 반 양자화 된다는 것이다.
이러한 반 양자화 현상은 크라머스 겹상태에 놓인 전자가 다녕ㄹ 수송될 때, 한 주기 사이에 생기는 베리 선속이 2π가 아니라 π인데서 기인한다.
일반적인 금속표면에서의 전자들은 물리적 경계, 즉 스텝을 만났을 때 후방산란을 한다.
하지만 위상학적 절연체(TSS시스템)에서는 후방 산란이 금지되어 있음을 알고 있다.
그렇다면 위상학적 절연체에서 전자들이 물질의 경계를 만났을 때는 어떤 행동을 보일까?
- Surface Conduction Channel = 효율적인 전자 수송
- Spin Momentum Locking = 스핀 제어
- Backscattering Prohibited= 무한한 전도도
- Strong TI = Bi2Se3, Bi2Te3, Sb2Te3 ~3D / HgTe ~ 2D
- Weak TI = Stack of 2D Materials (Graphene, ...)
'Topological Insulator' 카테고리의 다른 글
| Magnetoresistance in Topological Insulator (0) | 2024.05.30 |
|---|---|
| Dirac Materials (0) | 2024.02.19 |
| Spin Momentum Locking (SML) (0) | 2024.02.14 |
| Weak Localization(WL)& Weak Anti-Loacalization(WAL) (1) | 2024.02.06 |
| MXene (0) | 2024.01.18 |

댓글