
참조문헌
- Dirac Materials in a MatrixWay, Arka Bandyopadhyay, Debnarayan Jana
1. Introduction
Massless Dirac particles [ <-> Conventional Fermions (obey the usual Schrodinger Hamiltonian) ]
- The interactions do not seem to play a major key role.
Controlling the electrons at Dirac nodes in the first Brillouin zone needs the interplay of sublattic symmetry, inversion symmetry, and the time-reversal symmetry.
In this article, we have used explicit fundamental symmetry to understand the basic features of Dirac materials occurring in three diverse systems in a compact $2 \times 2 $ matrix way.
2D 물질은 높은 anisotropy와 chemical functionality를 가지는 매우 얇은 나노물질이다. 이 물질들은 적절한 조절, 크기, 모양을 통해 매우 다양하고 이색적인 물리적 성질을 발현한다. Dirac 물질은 class of material who possess a unique Dirac-like cone type of low-energy band structure within the first Brillouin zone (BZ). This allows for the production of extraordinary electrons that are distinctive from standard electron produced in metals.
일반적인 메탈 속에 존재하는 전자들은 massive particle처럼 행동하고, 에너지가 momentum에 대해 2차 함수 꼴로 나타난다. 이러한 massive electron들은 Schrodinger equation을 따른다고 한다. 반면에 Dirac electron의 경우, 에너지가 모멘텀에 대해 linear dependence를 가지며 Dirac 방정식을 따른다. Excitations in Dirac materials may be fermionic, bosonic or anyonic.
이 물질들의 특성은 doping, 그리고 field effect 셋업을 이용해 chemical을 바꿈으로서 조절할 수 있다. 이 문헌에서, 우리는 Dirac 물질(그래핀, 위상절연체, d-wave superconductor 등) 과 연관된 다양한 symmetry를 ($2 \times 2$) matrix representation을 이용하여 보고자 한다
2. Dirac cone in graphene-like materials
폴 디락은 역사적으로 위대한 업적을 남겼는데, 상대성이론과 양자역학을 통합한 것이 그것이다. 또한 스핀에 대한 개념과 반물질의 존재를 제안했던 것 역시 빠뜨리면 안된다. 더욱이, 그의 방정식을 이용하여 양자장론이라 하는 새로운 아이디어를 성공적으로 소개할 수 있게 됐다. 하지만, 그래핀의 발견은 응집물질 물리 분야에서 상대론적 Dirac 방정식 유효성에 관한 의문을 갖게끔 하였다.
그래핀의 nearest-neighbor tight-binding (NNTB) Hamiltonian은 아래와 같이 쓸 수 있다.

여기서 $i$, $i+1$ 은 그래핀의 A, B atomic sites의 label이다. Creation (annihilation) operator $c_i^\dagger $ ( $c_i $)는 i번째 자리에 전자를 생성(제거)한다. 다른 두 항 $\epsilon$과 $t$는 각각 on-site potential energy와 pristine graphene의 hopping parameter를 나타낸다.

Momentum space에서, 위 방정식은 아래와 같이 matrix form으로 나타낼 수 있다.

위 행렬에서, on-site potential enegy ($\epsilon$)은 0으로 가정해다. 이는 Fermi energy를 0 레퍼런스 값으로 이동하는 것과 같다고 볼 수 있다. 위 식의 off-diagonal 항은 아래와 같이 쓸 수 있다.

여기서 $\delta_i (i \in \{1,2,3\})$는 nearest-neighbor vector이며, Fig.1과 같이 아래의 값을 갖는다.
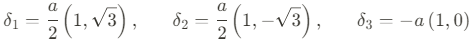
위 NNTB Hamiltonian의 eigenvalue는 그래핀 시트의 energy dispersion 관계를 나타낸다. Eigenvalue는 아래와 같이 쓸 수 있다.
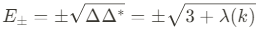

위의 dispersion relation은 Fig.1(c)에 묘사되어 있다. Conduction band와 valence band는 BZ( $K$ and $K'$)의 코너에서 서로 맞닿아있으며 zero band hap semiconducting 또는 semi-metallic 행동을 보인다. 이는 다음의 arguments를 통해 이해할 수 있다. $K$와 $K'$의 좌표는 각각 $\cfrac{2\pi}{3\sqrt{3}a}(\sqrt{3},1)$, $\cfrac{2\pi}{3\sqrt{3}a}(\sqrt{3},-1)$ 이다.
$K$와 $K'$에 대해서 $k_x$와 $k_y$의 값을 각각 빼주면 우리는 $\lambda(k)$ 값이 -3으로 불변함을ㅇ ㅏㄹ 수 있다. 결과적으로, $E_\pm$은 $K$와 $K'$에서 0이다.
행렬 꼴은 아래와 같이 더욱 명시적으로 작성할 수 있다.
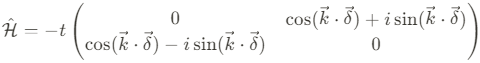
Band touching point $K$와 $K'$에서, 위의 방정식은 아래와 같이 간소화 시킬 수 있다.
우선 상대적 모멘텀을 나타내는 두개의 파라미터 $q(q_x, -q_y)= \kappa- K$와 $q'(q_x, -q_y)= \kappa- K'$ 를 정의하면, Hamiltonian은 아래와 같이 쓰일 수 있다.

위의 방정식은 $K$와 $K'$ point 부근에서 Pauli spin matrices ($\sigma = (\sigma_x, \sigma_y)$)를 이용한 간소화된 형태로 다시 쓸 수 있다.
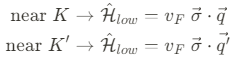
이때의 low energy Hamiltonian $\hat{\mathcal{H}}_{low}$는 상대론적 Dirac Hamiltonian $\hat{\mathcal{H}_D$와 효율적으로 비교할 수 있다.
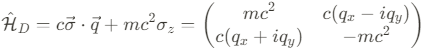
이 Hamiltonian의 eigenvalue는 아래와 같으며, gapped states를 결과로 내놓는다.

하지만, 다음의 차이점이 관찰된다.
- 응집물질 시스템 내에서, 속도는 빛의속도가 아니라 Fermi velocity ($v_F$)로 나타난다.
- Pristine graphene의 경우 질량 항이 0이다.
위의 상대론적 Dirac Hamiltonian으로 묘사할 수 있는 quasi particle은 Dirac fermion으로 널리 알려져 있다. Massless Dirac equation ( $m \rightarrow 0$)의 경우, energy spectra는 gapless 형태를 띄며, dispersion relation은 linear하다. 이 특징은 일반적인 금속 또는 반도체의 dispersion relation(2차항)과 다른 것이다.
금속, 그리고 몇몇의 도핑된 반도체에서는 low energy Schrodinger Hamiltonian ($\mathcal{H}_S$)는 아래와 같이 쓸 수 있다.

여기서 $m^*$는 particle의 effective mass를 나타낸다. 이러한 묘사를 따르는 quasiparticle을 Schrodinger fermion이라 한다.

더욱이, 위의 Dirac Hamiltonian 공식에서 보면, massive Dirac Hamiltonian의 양의 에너지 eigenstates와 음의 에너지 eigenstates는 똑같은 space of spinors로부터 만들어진다. 이로인해, particle과 hole은 똑같은 effective mass를 공유하고 이는 결과적으로 band gap $\Delta = 2mc^2$을 성립시킨다.
또한, 일반적인 금속과 부도체에서는, particle과 hole이 상호연결되어 있지 않으며, 분리된 상태로 각자의 Schrodinger equation을 따로 만족한다는 것을 기억하자. 이는 particle과 hole에 대한 서로 다른 effective mass를 갖게끔 하고 band gap에 대한 특별한 제한이 없다.
STM은 DOS를 실험적으로 측정할 수 있도록 한다. 요약하자면, 모든 gapless semiconductor는 Dirac material이 아니다. 2D 물질과 2D Dirac 물질의 차이는 Fig.2에 나와있다. Energy-momentum relation이 포물선의 dispersion을 갖는 이상, 그들은 Fig.3.에 나와있듯이 Schrodinger equation을 따른다. 하지만 Dirac material은, 물질 내 시스템에서 particle과 hole 언제나 상호연결(interconnected)되어 있으며, 상대론적 Dirac 방정식의 지배를 받는다는 점에서 특별하다.
As mentioned earlier, Dirac Hamiltonian in condensed mat ter systems contains the Fermi velocity instead of the speed of light. 더욱이, 그 값은 Lorentz covirant가 아니다. $\hat{\mathcal{H}}_D$에서의 spin operator는 입자의 실제 스핀을 나타내지는 않으며, 더 일반적인 degree of freedom을 나타낸다. 더욱이, Bosonic Dirac materials의 경우, 정성적으로 fermionic Dirac materials과는 다르다. 이전에 언급했듯이, fermionic Dirac materials은, Fermi velocity가 Dirac velocity와 같은 경우인 fermionic quasiparicles이 있음으로써 특정된다. 다시 말하자면, bosonic Dirac maetiral 시스템에서는 Fermi velocity가 존재하지 않으며, Dirac velocity가 더 일반적인 key property가 되는 것이다.
Dirac materials에서 또 다른 흥미로운 특징을 보자면, 2D Dirac materials에서의 Landau level quantization은 field($\vec{B}$)의 크기에 선형적이지 않으며 Fig.4에 묘사 되듯이 아래의 관계를 따른다.
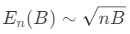

여기서, 금속이 비열이 온도에 따라 선형적으로 상승하는 low-energy electronic exciation에 대해서 유한한 phase-space를 갖고 있음을 알아두자. 하지만, 반도체는 electronic excitation에 의해 극복되는 finite energy gap으로 특정되어진다. 그러므로, 열에 의해 생성되는 EHP는 낮은 온도에서 기하급수적으로 억제된다. 일반적으로, 임의의 d-차원에서 dispersion relation 은 $E ~ k^S$꼴로 쓸 수 있다. DOS $g(E)$는 아래의 기초적인 계산을 통해 구할 수 있다.
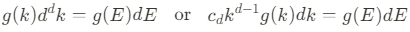
이때 오른쪽 식을 약간 변형하면
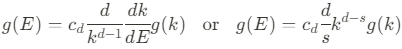
이는 아래의 경향성을 나타낸다.

다른 말로, d-차원에서 dispersion relation $E \sim k^s$에 상응하는 DOS는 바로 위 식과 같은 경향성을 나타낸다. 그러므로 DOS는 Dirac point에서 사라지며 이는 "d>1"에서의 필수적인 semi-metal의 특성을 나타낸다. 그래핀, 또는 TI와 같은 2차원 시스템에서는 DOS는 Fig.1(d)와 같은 V자 형태를 나타내며, $E=\hbar^2k^2/2m$의 dispersion relation을 보이는 massivep article이 상수로 평행한 DOS를 가지는 것과 대비된다. 그리고 평균 에너지 $U$는 아래와 같이 쓸 수 있다.

온도에 따른 $U$의 varation은 아래와 같다.

비열은 그저 샘플의 온돌르 변화시키기 위해 필요한 에너지인 점을 감안하면, low temperature 비열은 모든 임의의 공간적 d차원에서 $T^{d/s}$에 비례함을 짐작할 수 있다. 사실, Debye $T^3$는 d=3과 s=1 밸류를 따른다. 비록, 강자성 low temperature magnon의 specific C는 $T^{3/2}$에 비례하는데, 이는 다시 말해 d=3, s=2를 의미한다. Dirac 물질의 low temperature specific heat C는 온도가 0 K로 가까워 질 수록 $T^d$에 비례하는데, 금속의 경우에는 온도가 0 K에 가까워질 수록 C는 $T$에 비례해진다.
그러므로, 물리적 차원이 1보다 큰 시스템에서는 low temperautre specific heat에 대한연구는 결과적으로 Dirac 물질 속 quasiparticle에 내재된 본질을 증명하는데 도움이 될 것이다.
그래핀의 경우, 파라미터는 $d=2$, $s=1$이다. 그러므로, $U(T) \sim T^3$, $C_v \sim T^2$를 예상할 수 있다.
Here, it is important to note that the metals possess finite phase-space for low-energy electronic excitations where specific heat increases almost linearly with the temperature. However, semiconductors are characterized by a finite energy gap to be overcome for electronic excitations.
'Topological Insulator' 카테고리의 다른 글
| Magnetoresistance in Topological Insulator (0) | 2024.05.30 |
|---|---|
| Spin Momentum Locking (SML) (0) | 2024.02.14 |
| Weak Localization(WL)& Weak Anti-Loacalization(WAL) (1) | 2024.02.06 |
| MXene (0) | 2024.01.18 |
| (작성중) 위상부도체 (Topological insulator) (0) | 2021.05.24 |




댓글