참고문헌
- Spin Splitting of an Au(111) Surface State Band Observed with Angle Resolved Photoelectron Spectroscopy, S. LaShell
- 12312
Spin Momentum Lcoking은 spin의 방향이 carrier momentum의 방향과 correlated 되어 한 방향으로 고정(locking)되는 효과로, SOC가 강력한 물질에서 나타나는 현상이다.
그 중 대표적으로 topological insulaot에서 나타나는데, 이를 한번 살펴보겠다.
These results are interpreted as spin-split surface state bands, with the spins aligned in the plane of the surface perpendicular to the electronic momentum. The origin of the splitting is spin-orbit coupling, which can break spin degeneracy in systems which lack inversion symmetry
Spin-orbit Coupling과 같은 coupling은, 일반적으로 원자 속 전자의 degeneracy를 split하는 것으로 알려져 있다. SOC에 대한 Hamiltonian은 Schrodinger equation의 relativistic correction으로 얻을 수 있으며, 아래와 같은 식을 갖는다.

몇가지 approximation을 더하면, SOC는 $\vec{L}\cdot\vec{S}$에 비례하는 꼴로 바꿔 쓸 수 있으며, 이 항을 통해 twofold degenerate (spin only) level이 SOC에 의해 orbit에 parallel한 level과 antiparallel한 level로 나눠 짐을 짐작할 수 있다.
하지만, 이러한 splitting은 inversion symmetry가 보존되는 시스템에서는 금지되며, 대부분의 고체들은 SOC에 의해 깨지는 spin degeneracy가 없다.
결정 표면에서는 inversion center가 부재하므로, 이 symmetry를 깰 수 있으며 같은 평행한 wave vector $\vec{k}_{||}$를 가지며 반대 방향의 스핀을 가지는 surface state level이 서로 다른 에너지를 갖게끔 할 수 있다.
이 과정을 거쳐 나오는 slit bands의 구조는 nearly free electron(NFE) model을 통해 볼 수 있으며, 이는 surface state를 포함하는 가장 단순한 모델이다. NFE splitting의 크기는 형용할 수 없을 정도로 작으며, 이는 NFE에서 SOC가 가장 큰 영역인 ion core 근처 영역을 explictily 무시하기 때문이다. The qualitative behavior, however, appears to be correct for sp-derived surface states near the center of the surface Brillouin zone (SBZ) G.
Spin-orbit coupling in non-centrosymmetric crystals gives rise to interesting spin-momentum locking of the Fermi surface.
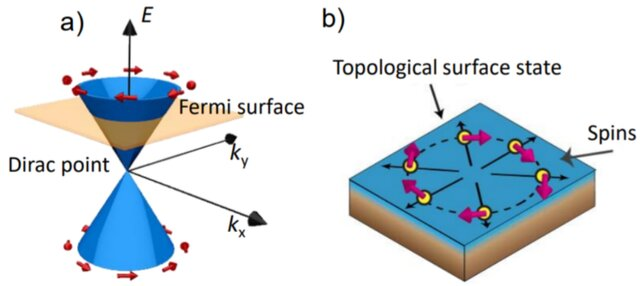
In solids, Rashba and Dresselhaus effects are manifestations of spin-orbit coupling [8]. SOC also
plays a significant role in the inverse Edelstein [9] and spin Hall [10] effects (where spin-polarized
currents can be generated in the absence of external magnetic fields) and it is the key ingredient
to understand topological insulators and the quantum spin-Hall effect.
자기장이 없는 물질에서는, 전자와 홀의 spin degeneracy는 SIS와 TRS의 결합된 효과이다. 이는 수식 $E_\uparrow(\vec{k}) = E_\downarrow(\vec{k}) $으로 나타낼 수 있다. 하지만, 만약 전자가 inversion symmtetry가 깨진 potential 속에서 이동하는 경우, spin degeneracy는 외부 자기장이 없음에도 깨질 수 있다. 이 경우, 두개의 energy dispersion branche가 나타나며, 각각이 $E_\uparrow(\vec{k})$, $E_\downarrow(\vec{k}) $이다.
Another way to lift the degeneracy of the energy bands is through a structural inversion symmetry
breaking. As an example, we take an asymmetric quantum well, lacking an inversion center in
the growth direction.
For two-dimensional electron gases with electric fields along the z direction (for instance, a top
gate electrode), the effective magnetic field Beff is both perpendicular to the carrier velocity
and the electric field (see Eq. (2.4)). This SO-induced magnetic field will couple to the electron
spins and, therefore, the spins of the carriers are coupled perpendicularly to its momentum. The
Rashba Hamiltonian can be written as [2]
$E_{+}$와 $E_{-}$의 energy splitting은 Fig.2.2a에 나와있다. 이 figure에서, $E_0$는 SOC가 부재할 때의 degenerated energy band를 나타낸다. Fermi energy $E_F$에서 각각의 Fermi contour(effective magnetic field의 방향과 평행)는 Fig.2.2b에 나와있다.

Both Dresselhaus and Rashba SO couplings generate a “spin-momentum locking” of the electron
spin to its linear momentum and lift the spin degeneracy of the energy bands. Both Rashba
and Dresselhaus spin-orbit effects will be discussed in more depth in Chap. 4 in order to study
anisotropies in the magnetoresistance of HgTe in the presence of in-plane magnetic fields.
'Topological Insulator' 카테고리의 다른 글
| Magnetoresistance in Topological Insulator (0) | 2024.05.30 |
|---|---|
| Dirac Materials (0) | 2024.02.19 |
| Weak Localization(WL)& Weak Anti-Loacalization(WAL) (1) | 2024.02.06 |
| MXene (0) | 2024.01.18 |
| (작성중) 위상부도체 (Topological insulator) (0) | 2021.05.24 |




댓글