The spin current vorticity (SCV) of the Fermi sea.
The circulation of spin currents about the Fermi surface.
스핀 소용돌이는 reciprocal space에서 발생하기에, real space에서 localization 되지 않으며, defects 같은 scattering center로서도 작동하지 않는다. 오히려 overall cortical background로서 작동한다.
이를 수학적으로 다시 기술해보고자 하며, 아래의 내용을 인지하길 바란다.
비록 스핀 수송이 defects에서의 asymmetric scattering을 포함하지 않은 constant relaxation time approximation을 가정하고 이루어지며, 그렇기에 extrinsic skew scattering과 side jump contribution을 포함하지 않지만, MSHE는 scattering에 의한 것이 아니라 spin current 그 자체로서 chiral 하기에 포함된다.
SCV의 관점에서 보면, MSHE의 time-reversal odd nature는 vortex의 handedness 반전으로 쉽게 이해되며, 결과적으로 반대되는 deflection을 유발한다. 그러면, magnetic texutre의 reversal은 MSHE가 말들어낸 스핀류의 spin accumulation 방향도 반대로 뒤집어 버린다. (SHE spin currents는 영향받지 않음을 상기하자).
이 스핀류 소용돌이가 만약 존재할 수도 있다는 것을 보여주기 위해, 우리는 모든 magnetic Laue groups(MLGs) with repect to their compatibility with a nonzero SCV,를 분석했다. 이를 통해 모든 가능한 MSE 시나리오를 확인했다.
이 중 특히 단순한 한 시나리오는 강자성체 에서의 SOC: assuming a tetragonal ferromagnet with magnetization $\vec{M}$ in the z directionm 우리는 다음의 SCV를 발견했다.
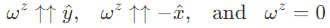
z spin component에 대해서는, Fermi sea는 MSHE를 ㅠ발하지 않는다. 반대로, x, y spin components에 대해서는 nonzero vorticies가 MSHE를 유발한다. 더 정확하게, x(y) spin component에 대한 MSHE는 xz(yz) plane에서 발생한다. 결과적으로, 이러한 강자성체는 nonozero antisymmetric parts of $\sigma_{\gamma z}^{\gamma}$ (and $\sigma_{z \gamma }^{\gamma}$) as long as $\gamma = x, y$; the transported spin componnet, the electric field, and the flow direction of the spin current lie within a plane that contains the magnetization. 이것이 MSHE spin currents가 pure한 이유이다: z방향 자화에 상응하는 transverse AHE charge currents는 오로지 xy plane에서만 흐른다.
SHE와의 차이점을 좀 더 명확하게 하기 위해, 자화($\vec{M} \parallelto \hat{z}$)와 평행한 방향으로 전기장이 작용하는 경우를 가정해보자. Conventional SHE의 spin conductivty tensor elements 떄문에, (antisymmetric) spin은 sample의 surface plane에 축적된다 (파란색 화살표). 이때 축적되는 spin의 polarization 방향은 surface normal과 전기장에 서로 직교한다. 또한 time-reversal even이기에, 자화의 방향이 바뀌어도 spin polarization은 그 방향을 유지한다.
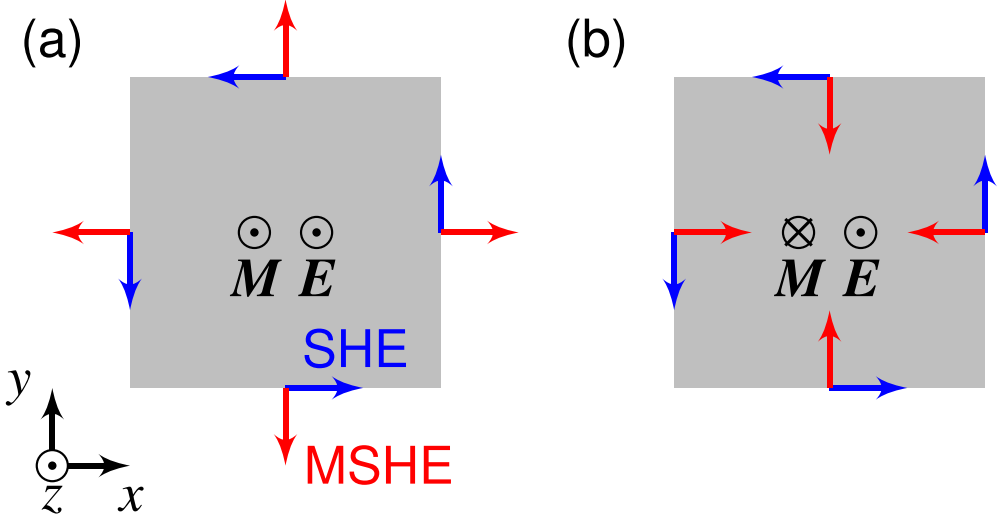
반대로, MSHE($\sigma_{xz}^{x} = \sigma_{yz}^{y}$)는 추가적인 accumulation을 유발하며, 이 때의 spin polarization의 방향은 surface plane에 수직한 방향이다(빨간색 화살표). 또한 이 MSHE는 time-reversal odd이므로, magnetization의 방향이 바뀜에 따라 spin polarization도 그 방향이 뒤집한다.
그러므로, MSHE는 CSHE의 spin accumulation과 수직한 방향으로의 spin accumulation을 유발한다. . In scenarios in which the magnetization of the ferromagnet is fixed, this feature may result in the decisive spin accumulation direction necessary to perform a particular spin torque switching. 예를 들어, 이전 수직자화 박막의 field-free magnetization switching은 이 MSHE에 의한 spin accumulation으로 설명할 수 있을 것이다. 우리는 spin current vortices의 존재는 bulk MSHE spin current를 만들어내어, 계면이나 edge에서 spin accumulation을 유발하는 bulk property임을 강조한다.
That the SHE and MSHE cause spin accumulations pointing in orthogonal directions is a speciality of the MLGs $4/mm'm'$, $4'/mm'm$, and $m'm'm$, which allow for the “clearest” disentanglement of MSHE and SHE. For other MLGs there is at least one element of the spin conductivity tensor that carries simultaneously contributions from the SHE and the MSHE, leaving the behavior under time reversal (texture reversal) as the only distinguishing characteristic.
이때, 3차원 강자성체는 제쳐두고, 2DEG이 매우 매력스럽게 보인다. 2DEG은 큰 Rashba SOC에 의한 효율적인 charge-to-spin conversion으로 잘 알려져있고, superconductivity와 섞인 자성, 그리고 전기적 controllability로 유명하다. 2DEG에서 상온 자성을 얻는데 있어서 최근의 progress는 이 시스템들에서의 MSHE에 대한 조사를 암시한다. 이를 위해, we consider a minimal Rashba Hamiltonian with warping and an exchange field whose direction provides a handle to switch between different MLGs.
평면 내에서 자기장을 회전시키면, 평면 내로 편극된 스핀의 MSHE가 조작될 뿐만 아니라 평면 밖으로 편극된 스핀의 MSHE도 조작된다. 이와 비슷한 결과가 Sn-doped $Bi_2 Te_3$, noncollinear antiferromagnet $Mn_3 Sn$ 과 같은 topological Dirac surface states에서도 적용된다.
The remainder of the paper is organized as follows. In Sec. III the theoretical framework within which we describe spin transport is introduced. We disentangle time-reversal even from odd contributions in Sec. III A, isolate the MSHE, and introduce the SCV interpretation in Sec. III B. Then, we turn to the symmetry analysis of all MLGs and summarize key findings in Sec. III C. These are elaborated on in Sec. IV by considering specific toy models; the latter serve to underline the minimal requirements for a nonzero MSHE (Sec. IV A), to make connection to magnetized Rashba materials (Sec. IV B), and to demonstrate the magnonic MSNE (Sec. IV C). We discuss the relation of our work to literature in Sec. V and summarize in Sec. VI.
III. Linear-Response Theory of the Mangetic Spin Hall Effect
The optical spin conductivity tensor는 Kubo linear-response theory에서 아래와 같이 쓸 수 있다.
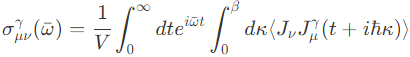
A. Decomposition of the spin conductivity tensor
우리는 crystal momentum $\vec{k}$ representation에서 Hamiltonian에 의해 기술되는 non-interacting 전자들로 한정하여 보고자 한다.

$\psi_{\vec{k}}^\dagger ( \psi_{\vec{k}}^)$는 electronic creation (annihilation) operation이다; its index runs over spin, orbitals, and basis lattice sites.
The eigenenergies $\varepsilon_{n \vec{k}$와 이에 상응하는 eigenvectors는 $ |n\rangle = | u_{n \vec{k}} \rangle$ 이며, band index n을 가지는 Bloch wave function의 lattice-periodic part를 나타낸다. 그리고 이 고유벡터와 고유에너지는 Hamiltonian kernel $\hat{\mathcal{H}}_{\vec{k}}$을 diagonalization 함 으로써 얻을 수 있다.
이 때의 dc spin conductivity는 아래와 같다.



여기서 $f_{n\vec{k}} = \left( e^{\beta(\varepsilon_{n \vec{k}}} - \varepsilon_F) + 1 \right)^{-1} $ 는 Fermi energy $\varepsilon_{F}$에서의 Fermi distribution function이다.
'Spin Hall Effect in Ferromagnets' 카테고리의 다른 글
| Origin of the magnetic spin Hall effect: spin current vorticity in the Fermi sea (0) | 2025.03.20 |
|---|---|
| DERIVATION OF REFLECTIONAND TRANSMISSION MATRICES (0) | 2024.04.23 |
| Interfacial spin-orbit coupling (0) | 2024.04.05 |
| The Spin Hall Effect (0) | 2023.10.30 |
| (작성중) Spin Hall effect in Ferromagnets (0) | 2023.04.11 |



댓글