Thin Film

참고 문헌

[1] Fundamentals of Ferromagnetism, Getzlaff

4.1 Single Thin Film on a Substrate

얇은 박막에서의 자화는 필름 내의 consant magnetic moments에 의해 특정되어진다. 하지만 박막의 양쪽 계면에 의해 deviation이 발생한다. 박막과 기판 사이의 계면에서 원자들의 electronic states의 hybridization이 발생하고, 결과적으로 magnetic moments의 감소로 이어진다. 표면은 증가된 magnetization을 보이는데, 이는 coordination number의 감소 때문이다. (예를 들어, atomic-like behavior가 우세하다). 온도가 증가함에 따라 박막 전체에 자화가 감소하는 경향을 보인다. 이 경향은 박막의 안쪽 layer보다는 계면과 표면에서 더 크게 발생한다. 중요한 파라미터는 역시 박막의 두께일 것이다. 이것이 anisotropy, Curie temperature, (spin dependent) transport properties, 그리고 quantum well등에 어떠한 영향을 끼치는지 의논해보고자 한다. 

Fig. 14.1. Schematic illustration concerning the variation of the magnetic moment m per atomic layer near an interface to a substrate and near the surface at T = 0 and T > 0

 

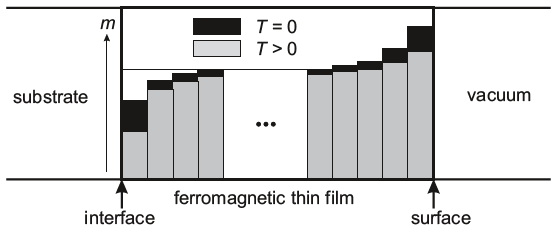
Anisotropy에 끼치는 영향

서로 다른 박막 두께에 따른 anisotropy의 변화는 이미 챕터 7.6에서 다뤘다. Effective anisotropy constant는 다음과 같다.

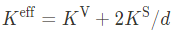
with d being the thickness of the thin film opens up, e.g., the possibility of a spin reorientation transition from an in-plane to a perpendicular magnetization with increasing thickness.

Curie 온도에 끼치는 영향

박막 시스템에서, Curie temperature $T_{\mathrm{C}}$는 일반적으로 bulk에 비해서 감소하는 경향을 보인다. 예를 들어 Re(0001) 표면 위에 증착된 Ni(111) 박막의 경우, 아래 그림과 같이 $T_{\mathrm{C}}$가 낮아진다.

Fig. 14.2. Saturation magnetization of Ni(111) films on Re(0001) as a function of temperature with the number of atomic layers d as parameter. The data were taken with increasing (closed symbols) and decreasing temperature (open symbols). (Reprinted from [47]. Copyright 1984, with permission from Elsevier)

This reduction is due to the absence of magnetic neighboring atoms. A quantitative description can be
given using a finite-size scaling model which results in:

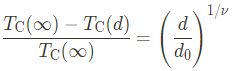
Critical exponent $\nu = 0.7$은 anisotropy에 대해 의존성이 거의 없다. Cubic system의 경우, normalized Curie 온도 $T_{\mathrm{C}}(d)/T_{\mathrm{C}}(\infty)$는 아래 Fig. 14.3과 같이 두께의 함수에 대해 uniform한 경향을 보인다.

Fig. 14.3. Normalized Curie temperatures as a function of the atomic layers d for different densely packed cubic transition metal films (Reprinted from [48]. Copyright 1993, with permission from Elsevier)

전체적인 곡선 The full curve represents a fit to the Re(0001)/Ni(111) data by a power law. The critical thickness d0 amounts to nearly two atomic layers. It is characterized by the minimum thickness which exhibits the loss of magnetic order already at T = 0K. But, (14.2) is not more valid for such thin films. Therefore, already the monolayer (d = 1) is often ferromagnetic. 

스핀 수송 특성에 끼치는 영향

강자성체 박막 내에서 움직이는 전자의 감소하는 세기 $I$는 운도에너지에 의존한다. 이 함수는 물질과 거의 독립적이며, 그러므로 어느 물질에서나 동일한 경향성을 가진다. Inelastic mean free path $\lambda$는 아래와 같이 주어진다.

이때 세기는 자성 박막의 자화와 연관이 되는데, 이는 spin-up 전자, 그리고 spin-down 전자 각각에 특정되어지는 inelastic mean free path $\lamba^{+}$, $\lamba^{-}$에 연관된다. 주어진 운동에너지에서 비자성 substrate의 interface를 떠나는 전자는 강자성체 박막의 자화와 평행한 경우와 반평행한 경우의 전자에서 모두 동일하다.  ($ I^{\up \down} = I^{\up \up} $)

Fig. 14.4. Inelastic mean free path λ given in monolayers as a function of kinetic energy for electrons in solids of various elements (black dots) (From [49]. Copyright 1979. Copyright John Wiley & Sons Limited. Reproduced with permission.)

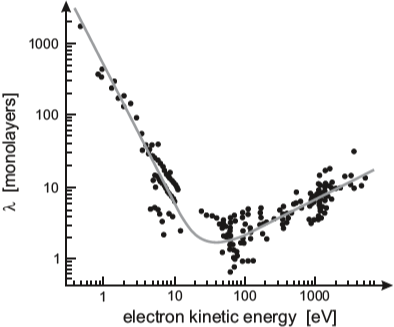
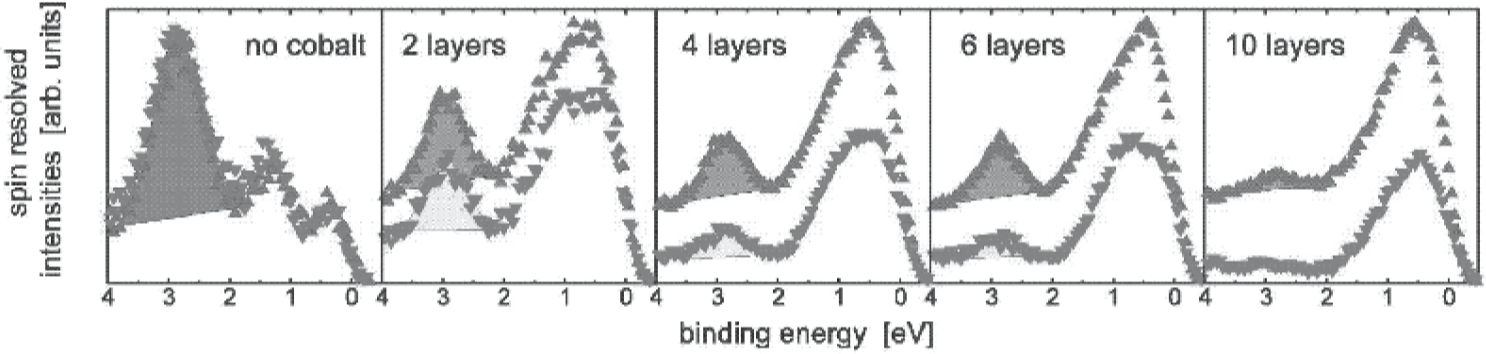
자성 박막을 지나고 나서부터는, 두 세기는 동일하지 않다. ($ I^{\up \down} \ne I^{\up \up} $).  아래 Fig 14.5는 W(110)기판 위의 자성 Co 박막에서 나타나는 P와 AP일 때의 전류 차이를 나타낸다. Electrons with a binding energy of 3 eV (below EF = 0) are only related to the substrate. After excitation with monochromatic radiation they pass several layers of ferromagnetic Co.We recognize that the intensity of the majority electrons is much less reduced compared to that of minority electrons. This spin filter effect is due to a spin dependence of the inelastic mean free path and is discussed on p. 227 in more detail. 

Fig. 14.5. Spin resolved photoelectron spectra for Co thin films on a W(110) substrate as a function of film thickness. The evaluated tungsten structures at a binding energy of 2.9 eV are shaded, the upper curve represents the majority and the lower curve the minority spin channel. The different intensities in the two channels are clearly visible at higher coverage. The peak areas which were obtained by integration assuming a linear background and indicated by light gray (for minority) and dark gray shaded areas (for majority electrons) allow to determine the inelastic mean free paths λ+ and λ− for spin up and spin down electrons, respectively

 

14.2 Influence of a (Non-Magnetic) Capping Layer

이미 Fig 14.1에서 봤겠지만, 강자성체 박막의 표면은 증가된 자기 모멘트를 보인다. 이때 비자성체 박막으로 캐핑을 하는 경우, 다음의 변화를 불어 일으킨다. 

• 표면 원자의 coordination number를 증가시켜 가장 상층부 레이어의 자기 모멘트를 감소시키는 결과를 보인다.
• 자성 박막 속 원자의 파동함수와 비자성체 캐핑 레이어 원자의 파동함수가 오버랩되어 hybridization을 유발하며, 결과적으로 가장 상층부 뿐만 아니라 계면 근처의 여러층에 대해 자기 모멘트를 감소시킨다. 
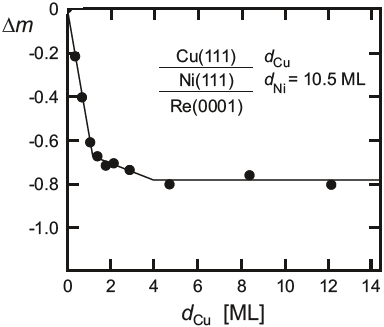
• 이 현상의 한 예로서, 자기 모멘트의 감소 $\Delta m$은 Fig 14.8에 나와있다. 해당 figure에는 Ni 박막이 여러 두께의 Cu film으로 캐핑되어 있다. Ni(111) 단일층에 대한 자기 모멘트의 감소는  Cu 캐핑 레이어 단일층보다 조금 더 두꺼운 두께까지 발생하며, 결과적으로 79%가 감소하는 결과를 만들어낸다. 추가적으로, saturation 됨을 통해 해당 시스템에서는 연속적인 자기모멘트의 감소를 만들어내는 interdiffusion이 발생하지 않는다는 것을 알 수 있다.

Fig. 14.8. Change of magnetic moment Δm in units of the magnetic moment of one monolayer Ni(111) caused by Cu(111) on Ni(111) thin films with a thickness of about 10 monolayers on Re(0001) as a function of the thickness dCu of the Cu coating layer. (Reprinted from [51]. Copyright 1985, with permission from Elsevier)

 

14.4 Comparison Between an Ideal and Real Interface

실제의 계면이 자성 특성에 끼치는 영향은 아래 Fig 14.11 처럼 반자성 기판위에 강자성 박막이 올라간 경우를 예로 들어 설명하겠다. 우선 왼쪽 그림처럼 이상적인 계면에서 ferromagnetic coupling이 발생함을 가정하면, 6개의 uncompensated 스핀이 반자성체의 스핀을 따라 발생한다. 하지만 실졔 계면에은 이상적인 계면처럼 평탄하지 않다. 실제 계면의 roughness는 강자성체와 반자성체가 서로 반대방향을 향하는 상황을 만들어내며, 전체 면적에서 ferromagnetic coupling이 발생하는 것을 방해한다. 대표적으로 frustration(동그라미),  또는 domain wall(박스)이 발생하여 uncompensated spin의 숫자를 줄여버린다.

Fig. 14.11. (a) 이상적인 계면은 평탄하다. 계면에서 ferromagnetic coupling이 발생함을 가정하면, AFM을 가정 했을 때 6개의 알짜스핀이 발생한다. (b) 실제로는, 대부분의 계면은 울퉁불퉁하며, and exhibit steps which separate different terraces. Now, the ferromagnetic coupling across the interface cannot simultaneously be fulfilled. Thus, frustration (circles) and domain walls (white box) can occur which leads to a reduction of uncompensated spins, in this example from six to two

 

14.5 Exchange Bias

기본적인 학습과 응용을 위한 가장 흥미로운 계면중 하나는 강자성체와 반자성체 사이의 계면이다. Fe와 같은 강자성체는 매우 큰 exchange parameter를 보여주지만, 상대적으로 작은 anisotropy를 가진다. 이것이 높은 온도에서도 ferromagnetic order를 안정적으로 만들어 주지만, 방향은 아닐 것이다. 특히, 수 나노미터의 박막이라면 말이다.   

Fig. 14.12. Shifted hysteresis loop in an exchange biased ferromagnet. Characteristic fields are the exchange bias field, HEB, and coercivities, Hc1 and Hc2

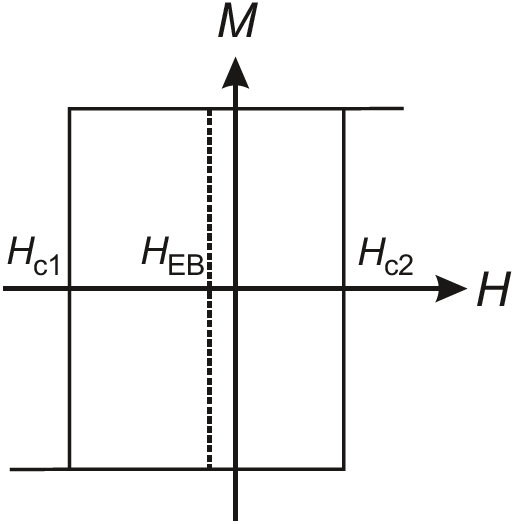
대부분의 강자성체들은 큰 anisotropy를 가지며, 결과적으로 매우 안정적인 방향성을 갖게된다. 강자성체와 반자성체 heterostructure에서의 excahnge coupling은, 원칙적으로, 강자성체와 같은 행동을 만들어내며, 이는 다시 말해 안정적인 ferromagnetic order에 더해 높은 anisotropy까지 추가됨을 말한다. 이러한 구조에서 anisotropy는 unidirectional 또는 uniaxial과 같이 행동할 것이다. 이 현상은 강자성체에서 발생하는 현상은 아니며 exchange bias라 불리는데, 여기서 bias를 붙이는 이유는 강자성체/반자성체 구조의 hysteresis loop를 그려보면 자기장이 0이 아닌 곳($H_{\mathrm{EB}}$)에서 중심점을 형성하기 때문이다. 

이 '옮겨진' hysteresis loop의 예는 Fig. 14.12에 나와있다. Hysteresis loop의 중심점은 $0$에서 $H_{\mathrm{EB}}$만 큼 옮겨져 있으며, 이때 이 $H_{\mathrm{EB}}$를 exchange bias field라 한다. Bias를 characterize하는데 3개의 서로 다른 field가 사용된다: 왼쪽, 오른쪽의 coercive fields $H_{\mathrm{c1}}$,  $H_{\mathrm{c2}}$, 그리고 bias field $H_{\mathrm{EB}}$이다.

이러한 shifted hysteresis loop은 아래와 같은 방법으로 얻을 수 있다.

1. 강자성체의 자화를 saturation 시키기 위해 한쪽 방향으로 자기장을 가한다.
   (이때 온도는 반자성체의 Neel temperature보다 높아야 한다.)
2. 이후 자기장을 유지한채 $T_{\mathrm{N}}$보다 낮게 온도를 내린다.
3. Hysteresis loop의 shift은 cooling을 한 이후에 측정 하는 경우 나타날 것이다. 

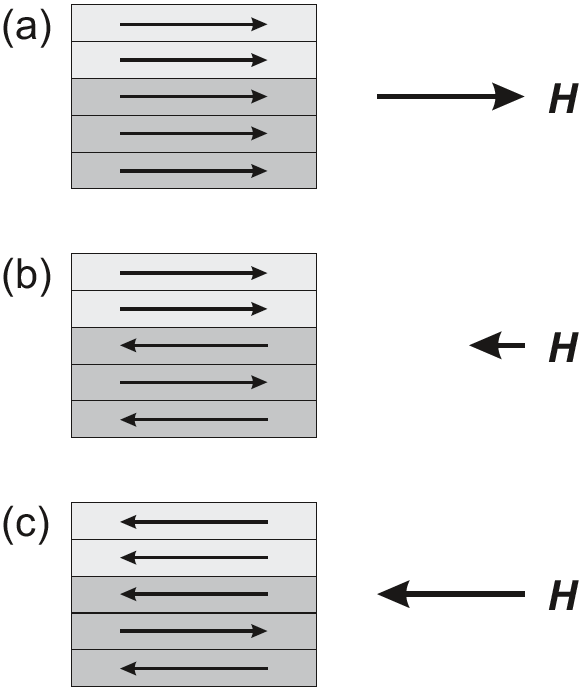
이 shift는 반자성체의 큰 anisotropy와 강자성체, 반자성체 사이의 약한 exchange energy coupling 때문이다. 해당 과정에 대한 schematic diagram은 아래 Fig.14.13에 나와있다. Fig.14.13(a)에서, 자기장은 $T_{\mathrm{N}}$보다 높은 온도에서 인가된다. 이는 강자성체 속 스핀을 모두 한 방향으로 정렬시킨다. 자기장을 계속 인가한 채 시스템의 온도를 $T_{\mathrm{N}}$ 이하로 낮추면, 반대방향으로 약한 자기장이 걸린다 하여도 자화는 원래의 방향을 계속 유지할 것이다.(Fig.14.13(b)). 이제 반대방향으로 interlayer exchange를 이겨낼 정도로 매우 큰 자기장을 가하면, 강자성체의 자화 방향이 역전된다.(Fig.14.13(c)). 이제 다시 반대방향의 자기장을 약하게 하면, 강자성체는 다시 원래의 방향으로 자화 방향을 바꿀것이다. 이 위의 과정을 한 그림으로 나타낸게 Fig.14.12이다. 

Fig. 14.13. (a) A saturating magnetic field is applied in order to align the ferromagnet above TN. After cooling the system in field the magnetization remains pinned along the original direction when the field is reversed as shown in (b). A sufficiently large field reverses the ferromagnet as shown in (c)

Shift의 정도는 interlayer excahgne와 연관된 effective field와 같다. Hysteresis loop은 anisotropy가 강자성체에 포함 될 때 나타난다. Coercive fields $H_{\mathrm{c1}}$, $H_{\mathrm{c2}}$는 단위 면적당 에너지의 stability를 계산함으로써 얻을 수 있으며, 이때 식은 아래와 같다. 

(14.4)

해당 모델에서 In this model the applied magnetic field is H, MS is the saturation magnetization
of the ferromagnet, dF the thickness of the ferromagnetic film, J
the interlayer exchange constant between the ferromagnet and the antiferromagnet,
and K a measure of the uniaxial anisotropy in the ferromagnet. The
angle θ is taken between M and the uniaxial anisotropy easy axis. 

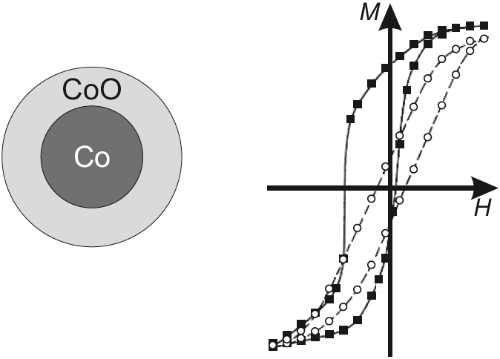
필드는 용이축 방향으로 향하고 있고, 자화는 해당 모델에서 균일함을 유지됨을 가정한다. 가장 중요한 restriction은 반자성체가 해당 물질의 용이축 방향으로 정렬되어 있으며, 이때 반자성체의 용이축과 강자성체의 용이축이 평행하다는 것이다. 실험적으로, CoO 코팅을 한 미세 Co 입자에서 exchange anisotropy가 발견 됐었다. CoO는 N'eel 온도 $T_{\mathrm{N}} = 293 K$를 가지는 반자성체이다. 이 입자들을 saturation magnetic field가 가해지는 상황에서 300 K (CoO가 상자성 상태일 때)에서부터 쿨링다운 시켜 77 K 까지 낮추면(CoO가 반자성 상태) unidirectional anisotropy를 관측할 수 있었다. Fig 14.14의 오른쪽 부분에서 발견된 두개의 hysteresis loop는 77 K에서 나타났다.

CoO가 코팅된 Co 입자들은 우선 첫번째로 상온에서부터 77 K까지 외부 자기장이 없는 상태에서 쿨다운 됐다. 이에 따른 hyseresis loop (dashed line으로 그려진 것)는 y축에 대해 대칭적이었다. 그 다음으로, 강한 자기장을 걸은 상태(이른바 field cooling)에서 77 K까지 쿨다운 시키면, hysteresis loop은 왼쪽으로 치우치게 된다.

Fig. 14.14. Left: Co particles being coated by CoO. Right: Hysteresis loops of oxide coated particles of Co taken at 77K. Open symbols show the hysteresis loop when the material is cooled in the absence of a magnetic field. The closed symbols show the hysteresis loop when the material is cooled in a saturating magnetic field. (Data taken from [53])

위의 방정식 (14.4)에 나오는 에너지는 $\theta = 0$과 $\theta = \pi$에서 극값을 가진다. $\theta=0$ configuration 일 때의 안정성은 아래의 조건을 만족할 때 성립하며,

$\theta=\pi$ configuration 일 때의 안정성은 아래의 조건을 만족할 때 성립한다.

이는 다음과 같은 coercive fields로 정리할 수 있다.

(14.5), (14.6)

Coercive fields는 크기가 모두 같지 않기 때문에, 최종적인 hysteresis는 biased된다. 이 모델에서 bias field는  hysteresis의 중간점으로 정의할 수 있다. 그렇기에 exchange coupling에 직접적으로 비례한다.

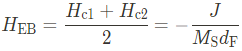
이 bias field는 Zeeman energy와 interlayer exchange energy 사이의 결쟁으로 정의되는데, 그러므로 강자성체의 두께 $d_\mathrm{F}$에 따라 값이 달라짐을 알 수 있다. Coercive field $H_{\mathrm{c}}$은 아래와 같이 주어지며, anisotropy constant $K$에 비례함을 알 수 있다.

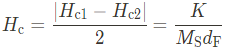
Hysteresis loop의 전형적인 온도 의존성은 아래 Fig. 14.15에 나와있다. 해당 figure의 structure는 Co/CoO로 이루어진 layered structure이다.

Fig. 14.15. Hysteresis loops for different temperatures of CoO(25˚A)/Co(120˚A). For each hysteresis the bilayer was cooled in a field of +2000 Oe from 320K to the respective temperature. (Adapted from [54] (used with permission))

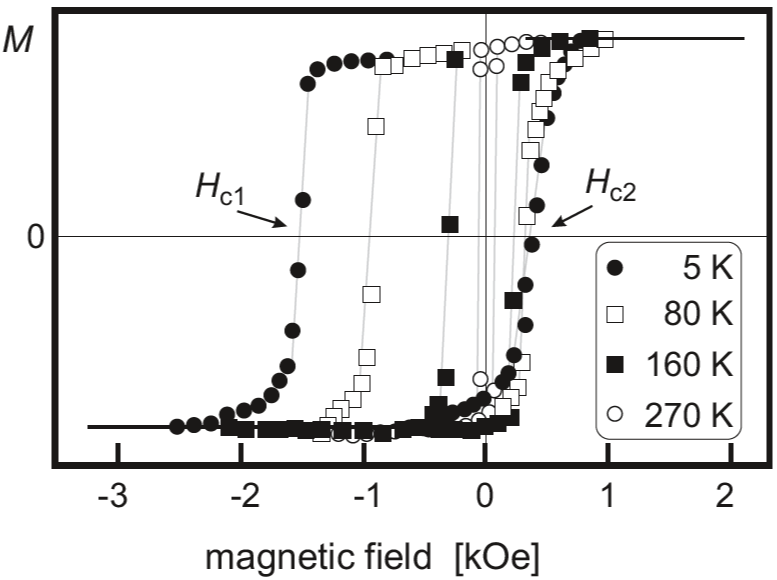
Hysteresis loop은 다음의 전형적이면서도 일반적인 특징들을 보여준다: $H_{\mathrm{c1}}$은 온도가 감소함에따라 매우 증가하는 반면에, $H_{\mathrm{c2}}$는 수백 Oe 정도의 값을 가지며 거의 변동이 없다. Hysteresis loop의 경사는 $H_{\mathrm{c1}}$이 $H_{\mathrm{c2}}$보다 더 가파르다. 

Figure 14.16은 비슷한 샘플에서 $H_{\mathrm{c1}}$과 $H_{\mathrm{c2}}$의 서로 다른 온도의존성에 대한 분석을 요약한 것이다. 두 coercive fields는 모두 Neel 온도 근방에서부터 같은 rate로 증가하기 시작한다.

at the lowest temperature. Thus, there are three distinguishable temperature
regimes.

First, from TN to TB the coercive fields are equal and increase slowly.
Second, close to TB the slopes increase drastically and Hc1 is slightly smaller
than Hc2. Third, below TB both coercive fields develop linearly but with
different slopes such that the absolute value of Hc1 is larger than Hc2. Only
in this last region a strong negative exchange bias is observed.
The dependence of the coercive fields as well as the exchange bias field
on the thickness of the ferromagnetic film dF is shown in Fig. 14.17. It is
obvious that all fields exhibit a 1/dF dependence which gives evidence that
the exchange bias effect is due to the existence of an interface.

Exchange bias와 관련하여 가장 주요한 특징들은 다음과 같다.

• 해당 현상은 반자성체 기판위에 있는 강자성체에서만 나타난다.
• 이 현상이 일어나기 위해서는 외부 자기장이 존재하는 상태에서 blocking temperature ($T_\mathrm{B} < T_\mathrm{N}$)밑으로 시스템을 쿨링 시켜야 한다.
• Unidirectional anisotropy는 field cooling으로 인해 발생한다.
• 일반적으로, exchange bias field는 음의 값을 가진다.
• Exchange bias field는 온도가 감소함에 따라 증가한다.
• Exchange bias field의 증가는 coercive fields의 증가를 야기시킨다.
• Exchange bais는 film thickness의 역에 비례한다. 

이번 챕터에서는, 여러층의 자성 박막으로 이루어진 다층박막 시스템에 대해 의논할 것이다. The principle arrangement consists of a ferromagnetic bulk-like or thin
film substrate covered by a non-magnetic thin film which itself is capped by
a ferromagnetic layer. This stacking may be continued by additional nonmagnetic
and ferromagnetic thin films. The non-magnetic layer consists of
a metal, an oxide, a semiconductor, or vacuum. The latter case stands for
two ferromagnetic electrodes which are separated by several˚A. An important
feature is given by the coupling over the interface, the so-called interlayer
exchange coupling (IEC).
Additionally, the electrical resistance or the electrical conductance of this
layered system depends on the relative orientation of the magnetization of
two neighbored ferromagnetic layers. The resistance of an antiparallel orientation
Rap is enhanced compared to a parallel alignment:

이 현상은 magnetoresistivity라 불리며, 16 챕터에서 더 자세히 의논할 것이다.

 

15.1 Interlayer Exchange Coupling (IEC) Across a Non-Magnetic Spacer Layer

비자성체 물질을 사이로 떨어져 있는 두 localized magnetic moments 사이의 coupling은 RKKY exchange interaction을 이용하여 설명할 수 있다.

여기서 x=2kFR�=2�F�이며, R�은 moments 사이의 거리이다. 이 oscillatory behavior는 Fig. 15.1에서처럼 실험적으로 묘사된다. 해당 figure는 Ge matrix속에 포함되어 있는 Mn 원자들에 대해 exchange constant J를 나타낸 것이다.

Fig. 15.1. Exchange interaction for Mn atoms as a function of their distance in Mn2Ge62. The solid line is the RKKY model fitted with kF = 1.02˚A &minus;1. (Adapted from [55] (used with permission))

이 의존성은 비자성 interlayer에 의해 분리된 자성 박막에 따라 달라진다. interlayer의 두께를 z라 하면, exchange coupling constant는 다음과 같은 경향성을 보인다:

Eq. 15.3

이는 Fig 15.2에 그림으로 나와있다. 이 처럼 interlayer가 존재하는 시스템에서는, RKKY 상호작용이 확연하게 나타나며, 긴 거리에 걸쳐 영향을 끼친다. J�가 양의 값을 갖는다는 것은 두 강자성체 박막 사이에 ferromagnetic coupling이 나타나는 것이고, 반대로 J�가 음의 값을 갖는 경우는 antiferromagnetic coupling이 나타남을 의미한다. 이처럼 우리는 spacer의 두께가 coupling의 종류를 결정함을 직접적으로 볼 수 있다.

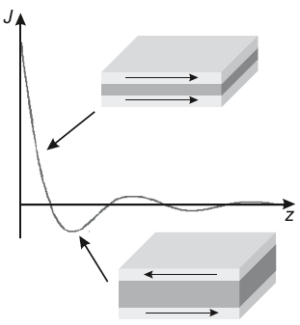
Fig. 15.2. Interlayer exchange coupling between two ferromagnetic thin films exhibiting an RKKY behavior. Depending on the thickness z of the spacer layer a ferromagnetic or antiferromagnetic alignment occurs for J > 0 or J < 0, respectively

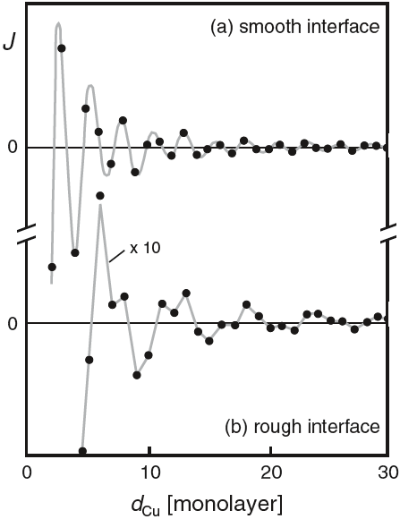
Fig. 15.3. Calculated interlayer coupling for a Cu(001) spacer as a function of the Cu thickness dCu at T = 0K. The solid circles correspond to physically achievable thickness, i.e. dCu integer. (a) Zero roughness, (b) rough interface. (Adapted from [56] (used with permission))

이 RKKY 상호작용에 대한 계산은 Fig 15.3과 같이 Co/Cu 시스템에 대해 깔끔한 표면과 거친 표면에서 어떻게 되는지 예제로서 나와있다. Figure 15.3(a)는 크고 짧은 주기의 진동을 보여주며shows
the calculated coupling exhibiting a strong short-period oscillation and a much
weaker long-period oscillation. 이때 레이어는 원자 단위로 평평함을 가정하였지만, 실제 시편은 언제나 계면에 rougness를 포함하고 있다. 이 roughness의 효과를 고려하기 위해, 평균 두께 d�의 spacer is assumed to consist actually of large (compared to the spacer thickness)
patches with local thickness equal to d − 1, d, and d + 1. 

이 가정한 상황에서의 coupling behavior는 Fig. 15.3(b)에 나와있다. coupling의 강도는 매우 감소하였고, 주기는 증가함을 알 수 있다. 이는 짧은 주기 대의 oscillation이 rougness에 의해 supressed 되어 오직 약한, 긴 주기의 oscillation만 보이기 때문이다. 이 단순한 예는 rougness가 얼마나 중요한 영향을 끼치는지 알려준다. The determination of the interlayer exchange coupling can only be carried out at positions of the discrete lattice planes. The thickness of the interlayer  amounts to: 

 

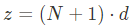
~241 p