참조 문헌
[1] Tomasz Dietl, EXHANGE INTERACTIONS: SUPER=EXCHANGE, DOUBLE EXCHANGE, RKKY; MAGNETIC ORDERS
[2] 송희성, 양자역학
1. Potential and Kinetic Exchange Interactions.
스핀과 관련된 상호작용을 설명할 때 쌍극자-쌍극자 상호작용이 주된 이유가 되기에는 너무 약하다는 사실은 매우 잘 알려져있다.
고체의 자기적 성질을 설명하는데는 두개의 스핀 교환 상호작용을 이용하면 매우 편하다.
우선 Potential exchange를 살펴본다.
Potential exchange는 Pauli의 배타원리에 기초한 교환 상호작용이다.
고전역학적으로 쿨롱력만을 고려하면, 전자는 모두 멀리 떨어져 자성체를 이루는 것을 선호할 것이다. 하지만 실제로는 높은 쿨롱력에도 불구하고 몇몇 전자는 서로 가까이 붙어 비자성체를 만든다. 이를 종합하여 exchange force라 하며, 이것이 어떻게 Pauli 배타원리와 이어지는지 아래에서 수식적으로 살펴보고자 한다. (Exchange force는 symmetrization 조건에 의한 순수 기하학적 결과이다. 또한 이는 명백하게 양자역학적 현상이며, 고전역학적 counterpart는 존재하지 않는다).
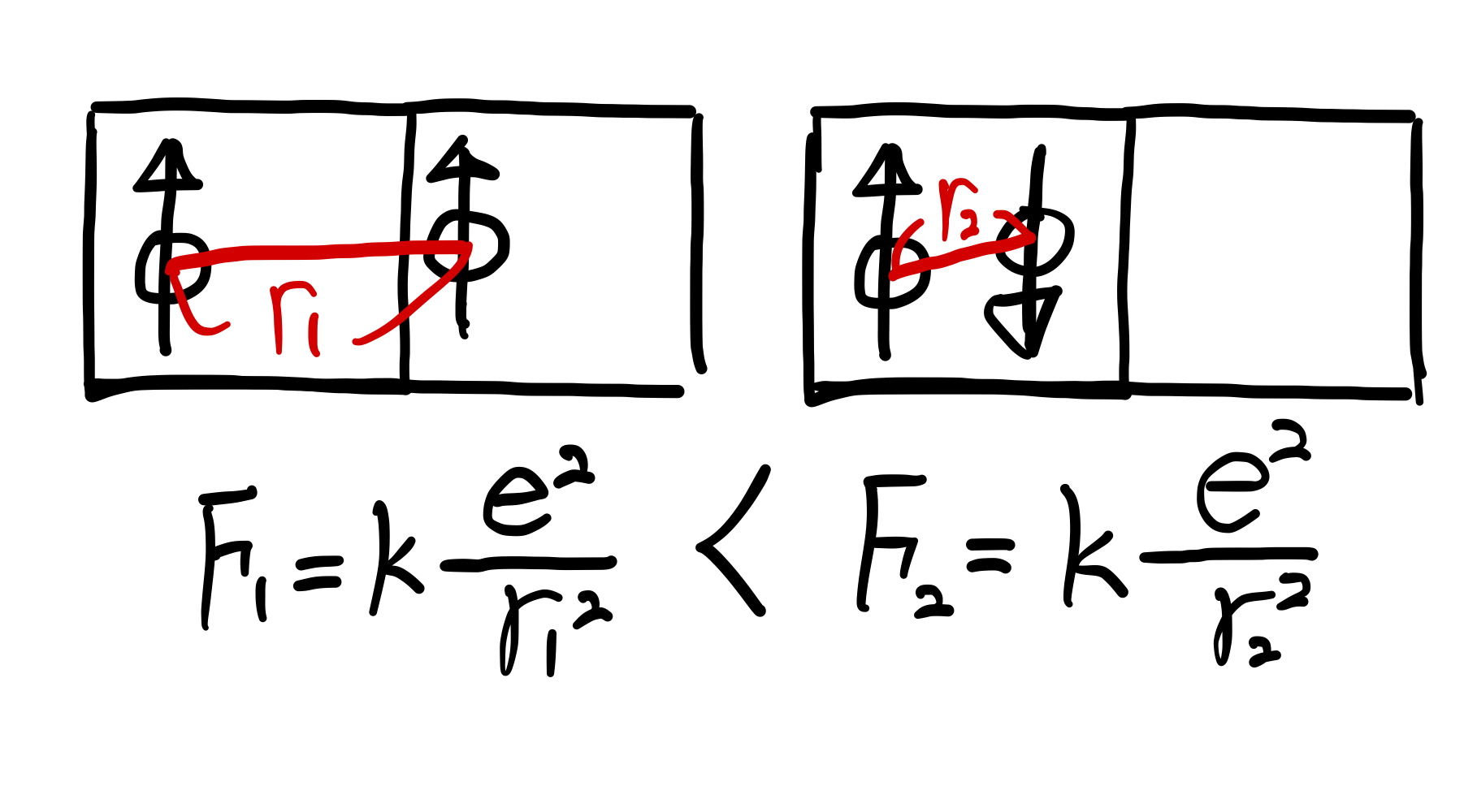
전자 1이 $\psi_a (x)$ state에, 또 다른 전자 2가 $\psi_b (x)$ state에 있고, 두 states가 서로 orthogonal 하며, 각각이 normalized 됐을 때, 두 입자사이의 거리제곱 $(x_1-x_2)^2$의 expectation value를 구해보면,
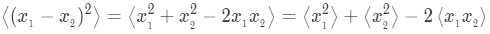
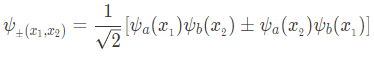
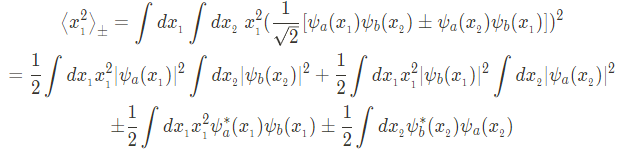
위에서 맨 마지막줄 두항은 orthogonality에 의해 소거되므로
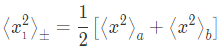
마찬가지로,
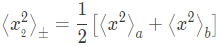
마지막으로
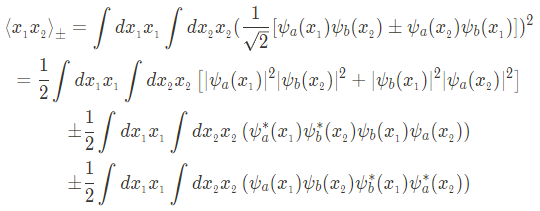
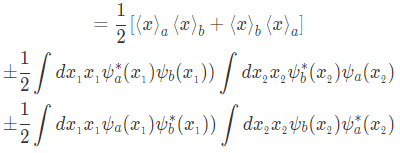
이때 아래와 같은 식을 정의하면
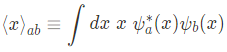
위의 나열한 식을 다음과 같이 정리할 수 있다.
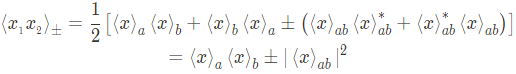
정리하면,

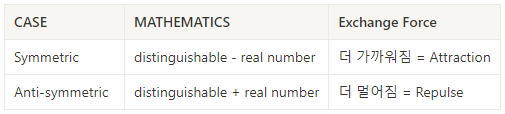
Spin을 포함하는 경우, wave function은 totally antisymmetric 해야하므로,
만약 spin이 antisymmetric 하다면, spatial part는 symemtric하다. 즉, singlet case에서 전자는 더 가까워지며,
spin이 symmetric 하다면, spatial part는 antisymmetric하므로, triplet case에서 전자는 서로 더 멀어진다.
수소의 경우, spin을 포함하지 않을 때 전자는 Fermion 특성 때문에 spatial antisymmetric하여 두 전자 사이에 repulsive force가 작용하지만, spin을 포함하는 실제의 경우, bonding을 이루기에 spatial part는 symmetric하며 spin이 singlet임을 유추할 수 있다.
Kinetic exhcagne는 서로 다른 위치의 전자 사이에 발생한다.
The kinetic exchange occurs between two electrons residing at different sites. One of these electrons can visit the site occupied by the other provided that its spin has the orientation matching a relevant empty level. Such a quantum hopping, or in other words hybridisation of states, enlarges the localisation radius and, hence, lowers the electron kinetic energy. The kinetic exchange leads usually, but not always, to an antiferromagnetic interaction between the spin pair in question. In compounds containing transition metals, the p-d kinetic exchange couples the spins of carriers occupying anion p-like bands with the spins of electrons residing in open d shells of magnetic cations. Typically, in the considered TM compounds the kinetic exchange – if symmetry allowed – is much stronger than the potential exchange. The opposite situation occurs in the case of rare earth doped materials, where the spd-f hybridisation is usually weak. Obviously, the way by which the above mechanisms lead to the spatial ordering of the spin polarisations depends on whether the d electrons remain localised on parent ions or undergo an insulator-to-metal transition and, therefore, contribute to the Fermi volume. In the former case, and in the absence of carriers, the spins of magnetic ions are coupled by the mechanism known as the superexchange. In metals or extrinsic semiconductors, where either conduction or valence sp bands are only partly occupied, a carrier-mediated spin-spin coupling emerges, known as the sp-d Zener or Ruderman-Kittel-Kasuya-Yosida (RKKY) mechanism. If doping of a magnetic insulator results in the appearance of electrons in the upper or holes in the lower Hubbard band, the so-called double-exchange mechanism can operate. Finally, for sufficiently large overlap between d wave functions the Mott-Hubbard transition will take place, so that the Stoner mechanism of ferromagnetism in an itinerant carriers systems will dominate. We will now briefly describe these mechanisms.
2. Superexchange
앞에서 언급된 sp-d 교환 상호작용의 결과로서, 가전자대의 전자들은 인접한 자성 이온에 의해 힘을 받을 것이다.
이때 인력인지, 또는 척력인지는 itinerant spin과 localised spin의 상호 방향에 따라 결정된다.
이는 가전자대에 존재하는 스핀-다운 전자와 스핀-업 전자가 공간적으로 재배치하는 결과를 불러 일으킨다, the total energy of the system attaining a minimum for an antiferromagnetic arrangement of neighbouring localised spins, as shown on Fig.1.
이러한 "직접적이지 않은" d-d coupling을 Superexchange라 한다.
사실 대부분의 자성부도체는 반강자성체이거나 페리자성체(if ions with differing spin states co-exist)이며, NiO의 경우 Neel 온도는 523K에 도달하고, Curie 온도는 80
This indirect d-d coupling is known as superexchange. Indeed, most of magnetic insulators are antiferromagnets or ferrimagnets (if ions with differing spin states co-exist), with Néel temperatures reaching 523 K in the case of NiO and Curie temperatures approaching 800 K in ferrimagnetic spinel ferrites (Zn,Ni)Fe2O4.
However, the case of europium chalcogenides (e.g., EuS) and chromium spinels (e.g., ZnCr2Se4) implies that the superexchange is not always antiferromagnetic and that ferromagnetism is not always related to the presence of free carriers, even though the Curie temperature TC does not exceed 100 K in these compounds, despite the large magnetic ion
concentration. In the case of rock-salt Eu compounds, there appears to be a competition between antiferromagnetic cation-anion-cation and ferromagnetic cation-cation superexchange [4]. The latter can be traced back to the ferromagnetic s-f coupling, and the presence of s-f hybridisation, which is actually stronger than the p-f hybridisation due to symmetry reasons [1,4]. In such a situation, the lowering of the conduction band associated with the ferromagnetic order enhances the energy gain due to hybridisation. The Cr-spinels represents the case, in which the d orbitals of the two cations are not coupled to the same p orbital, resulting – in agreement with the Goodenough-Kanamori rules – in a net ferromagnetic superexchange.
3. sp-d Zeneer/RKKY models
4. Double exchange
5. Stoner ferromagnetism
해당 글은 Hyper Physics 홈페이지에 게재된 Hydrogen Molecule 글을 해석한 글입니다.
Covalent bonding(공유결합)의 클래식 케이스, 수소 분자는 각 수소 원자가 가지고 있는 전자의 파동함수가 겹치는 현상을 형성한다. 이를 교환상호작용(exchange interaction)이라 한다. 이 결합의 특징은 NaCl처럼 이온 결합이 형성하는 특징과는 전혀 다르다.
If you measure then energy balance when you form H+ and H- ions and examine the attractive force between them, the energy required is positive for any value of ion separation.
That is, there is no distance at which there is a net attractive interaction, so the bond cannot be ionic.
수소 양성자 주변의 전자 분포는 양자역학적 파동함수로 나타낼 수 있다. 파동함수는 각 원자들이 가직 있는 전자를 설명하며, identical electrons의 exhcnage에 따라 symmetric이 될 수도 있고 antisymmetric할 수도 있다. Pauli exclusion principle에 따르면, 우리는 두개의 동일한 페르미온은 반드시 antisymmetric 이어야 한다는 것을 알 수 있다.
The electron spin part of the wavefunction can be symmetric (parallel spins) or antisymmetric (opposite spins), but then the space part of the wavefunction must be the opposite. That gaurantees that the entire wavefunction (the product of the spin and space wavefunctions) is antisymmetric. The two possibilities for the spatial wavefunctions for distant hydrogens are shown below.
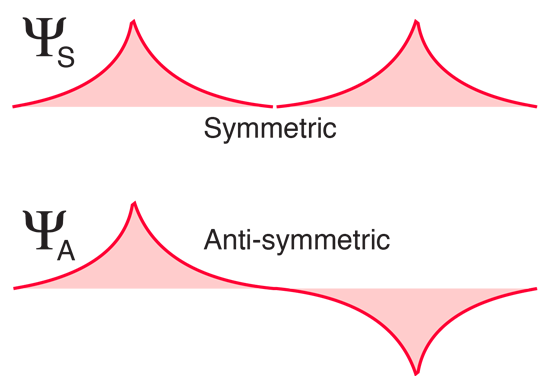
아래와 같이, 수소 원자들이 서로 붙을 때, symmetric spatial wavefunction은 전자의 bonding configuration을 유발하고, antisymmetric 의 경우에는 그렇지 않다. 실제 전하 밀도는 전자 파동함수의 제곱으로 나타나지므로, symmetric wavefunction이 핵 사이에서 더 높은 전자 밀도를 가지게 되며 atom 사이의 인력을 유발한다. $ \rightarrow $ bonding 형성
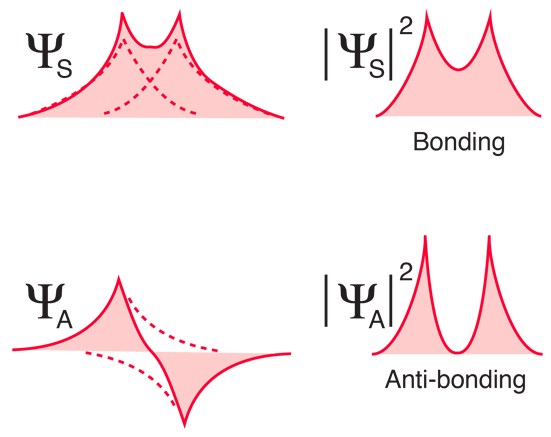
The exchange interaction (an entirely quantum mechanical effect) leads to a strong bond for the hydrogen molecule with dissociation energy 4.52 eV at a separation of 0.074 nm. The potential energy of the anti-bonding orbital shown gives some insight into why a third hydrogen atom cannot bond to the two atoms of the hydrogen molecule. It would be in an anti-bonding situation with one of the other hydrogen atoms and would therefore be repelled. We say that the bond in the hydrogen molecule is "saturated" because it cannot accept another bond.
'Other Topics' 카테고리의 다른 글
| Wavepacket (파속) in Quantum Mechanics (0) | 2023.03.13 |
|---|---|
| Eigenstates의 확률 진폭의 분포를 나타내는 두가지 방법 (1) | 2023.03.13 |
| (작성중) 밸리트로닉스 (Valleytronics) (1) | 2023.03.07 |
| Spintronics Measurement (1) : Harmonic Hall voltage measurements 를 이용한 스핀궤도토크 구하기 A to Z (1) | 2023.02.27 |
| (작성중) 오비트로닉스 (Orbitronics) (0) | 2022.08.29 |



댓글