이전 섹션에서, 우리는 공간적으로 변화하는 자기장 시스템에 대해 분석하고, adiabatic transport(스핀이 local magnetic tecture에 정렬된채로 유지되는)를 가정했을 때의 실제 공간상에서 Berry curvature가 나타남을 보였다. 이번 섹션에서는 현재 응집물리계에서 많은 관심을 끄는 주제, 다름 아닌 momentum space(또는 $\vec{k}$-space) Berry curvature에 대해 보고자 한다. 이전 장과 유사하게, 이 $\vec{k}$-space Berrry curvature는 $\vec{k}$-dependent magnetic fields(예를 들어 finite spin-orbit coupling)가 가해지는 시스템에서 존재한다.
A. Derivation of $\vec{k}$-space Berry curvature
일반적인 spin-orbit Hamiltonian은 다음과 같이 주어진다.

$\vec{k}$-space Berry curvature를 유도하기 위해서, 우리는 앞 섹션에서 썼던 방법인 unitary transformation을 다시 이용해보고자 한다. 그때와 마찬가지로, 우리는 $\vec{k}$-dependence를 "locking"하기 위해, 시스템에 local tranformation을 적용한다. 이 local transformation을 물리학적으로 보면 reference spin axis를 $\vec{B}(\vec{k})$의 방향으로 회전시키는 것이다. 이는 앞에서도 봤지만 unitary matrix $U=U(\vec{k})$를 통해 수행되며, 이 시나리오에서는 $(\theta, \phi)$는 $\vec{k}$-dependent 구좌표계이다. Unitary transformation을 거친 Hamiltonain은 다음과 같이 변한다.

위에서 포텐셜 에너지 항은 nontrivially transform 하는데, 이는 $\vec{r}=i\partial_k$은 $\vec{k}$-space derivatives를 나타내고, U는 $\vec{k}$의 함수이기 때문이다. 전기장에 의한 potential energy를 고려하면,

그러므로, coordinates에 대한 local rotation은 spatial operators의 정의를 아래와 같이 바꾼다.

위에서 $\mathcal{A}(\vec{k})$는 $\vec{k}$-space에서의 $2\times2$ gauge field이다.
Adiabatic limit에서, 우리는 오로지 $\mathcal{A}(\vec{k})$의 대각성분만 고려해도 됨을 알고 있으며, 이때 대각성분 각각이 SOC에 의해 발생하는 두개의 subband이다. 앞 섹션($\vec{r}$-space Berry gauge fields)에서 했던 계산을 똑같이 진행하면, 우리는 $\vec{k}$-space Berry gauge fields를 아래와 같이 구할 수 있다.

계속해서 $\vec{r}$-space 경우를 따라가면, $\vec{k}$-space 속 Berry curvature는 다음과 같이 구할 수 있다.

4334fdfdf
where ~n ¼ ~B=j~Bj is the unit vector pointing along the direction
of the spin-orbit field, ~Bð~kÞ.
또한 아래서 볼 예정이지만, curvature $\Omega_k(\vec{k})$는 $\vec{k}$-space에서의 유효 자기장을 나타내며, 캐리어의 궤도 움직임에 영향을 끼친다.
B. Physical Consequences
앞 장에서, 우리는 $\vec{r}$-space Berry curvature가 spin eigenstate-dependent Lorentz force를 이끌어 냄을 보였다. 여기서는, $\vec{k}$-space curvature 의 물리적 효과에 대해 기술하고자 한다. 증명 없이, Sundaram과 Niu에 의해 유도된 결과를 통해 이를 설명하겠다. 해당 유도에서는 $\vec{\Omega}(\vec{k})$가 존재할 때 wave packet의 준고전적 운동 방정식을 아래와 같이 기술한다.


위에서 첫번째 방정식은 carrier에 가해지는 힘과 관련된 식을 나타내며, 전기장에 의한 contribution과 $\vec{r}$-space에서의 Berry curvature를 포함하고 있다. 두번째 방정식은 wave packets의 속도에 대해 기술하며, 일반적인 group velocity항과 이에 더해 $\vec{\Omega}(\vec{k})$의 contribution을 포함하고 있다. 이 $\vec{\Omega}(\vec{k})$ contribution에 의한 것을 anomalous velocity라 한다. 명백하게, 이 anomalous velocity는 Lorentz force와 유사하며, 이 관점에서 봤을 때 $\vec{\Omega}(\vec{k})$를 $\vec{k}$-space에서의 Lorentz force라 할 수 있을 것이다.
역사적으로, $\vec{\Omega}(\vec{k})$를 포함ㅎ는 식은 Karplus와 Luttinger에 의해 1954년에 증명 됐고 이때는 강자성체에서의 anomalous Hall effect의 intrinsic contribution을 설명하기 위함이었다. 여기서, $\vec{\Omega}(\vec{k})$는 결정 속 momentum space에 내의 Bloch wavefunction으로 부터 나타난다. 하지만, 최근에야 topology와의 연관성이 화자되기 시작했다. 위에서 두번째 방정식은 $(\vec{k})$-space Berry curvature가 유한한 값을 가지는 응집 물질 시스템 속 vast array에서의 topological transport 현상을 묘사하며 아래에서 더 자세히 볼 예정이다.
B.1. Spin Hall effect
앞에서 우리는 스핀 방향에 의존하는 Hall-like separation 현상에 대해 기술했다. 이를 아래에서 공식화해보고자 한다. 우리는 전기장 $vec{E}_i$가 가해져 spin $s^{k}$가 전기장과 수직한 $\hat{j}$ 방향으로 흐르는 상황을 고려하고자 한다. Spin-Hall effect (SHE)에서는 $\hat{i}$, $\hat{j}$, $\hat{k}$ 가 상호 수직적인 관계를 가진다. 그러므로, 앞에서 기술했던 spin-dependent force $F_j= -\cfrac{2\alpha^2 m^2 v_i}{\hbar^3}\sigma^k$는 SHE의 한 예로 볼 수 있다. SHE의 세기는 spin-Hall conductivity(SHC)에 의해 정의되는데, 이는 수직한 스핀류 $j_{s,j}^{k}$를 전기장으로 나눠 아래와 같이 수식화 한다.

해당 장 섹션 C에서, 우리는 일반적인 SOC 시스템에서의 (spin) Hall conductivity를 구할 것이며, 이것이 본질적으로 $\vec{k}$-space Berry curvature와 이어져 있음을 증명할 것이다. 여기서 우리는 intrinsic SHE에 집중할 것이며 이는 band structure의 특성($\vec{k}$-space Berry curvature$)으로부터 나오는 현상이다. (Extrinsic SHE는 impurities에 의한 spin-anisotropic scattering에 의해 발생한다).
하지만, 반드시 짚고 넘어가야 할 점은, intrinsic과 extrinsic contributions 사이의 경계가 아직 명확하지 않다는 것이다. 특정 extrinsic SHE 메커니즘이 intrinsic 현상의 특성을 묘사하는데 발견되기도 하며, (scattering rate, impurity density의 dependency 등..) 더 나아가 $\vec{k}$-space Berry curvature와 연관되기도 한다.
현재는, intrinsic SHE는 많은 시스템에서 정량화가 됐으며, 주로 p-doped semiconductors 시스템을 예로 드는 경우가 많다. 이 시스템은 Luttinger Hamiltonian을 통해 모델링 되며, 이 Hamiltonian에서는 대부분의 반도체의 이중 축퇴된 valence bands에서의 spin-orbit splitting을 묘사한다.

위 식에서 $\gamma_1$과 $\gamma$는 valence-band parameter로서, effective hole mas를 정의한다. $\vec{S}$는 spin-3/2 matrices의 vector이다. 위 방정식에서 묘사하는 hole은 잘 정의된 chirality $\lambda = \vec{k}\cdot\vec{S}/\hbar|\vec{k}|$를 가지며, $\lambda = \pm1/2, \pm3/2$를 가진다. Hamiltonian에서는 내적 값에 제곱이 붙으므로, $\lambda$로 표현시에도 제곱을 갖게되며, 반대 부호를 가지는 chirality가 그러므로 degenerated되어, 이에 따라 two-fold degenerate light-hole (LH, $|\lambda|=1/2$), 그리고 heavy-hole (HH, $|\lambda|=3/2$) bands를 갖게 된다.
....
B.3. Magnon-Hall effect in ferromagnetic insulators
Spin-Hall effect와 비슷한 종류의 효과는 다른 wave에서도 예측됐는데, 대표적인 것이 강자성 부도체에서의 magnon이다. Magnon(또는 spin waves)는 자석 내에서의 low-energy excitation이며, band structure를 가지고 있다. 그러므로, 이 band structure에서도 Berry curvature가 발생할 여지가 있다. Berry curvature의 효과는 magnon의 준고전적 운동방정식을 통해 기술된다.


위 식에서 $U(\vec{r})$은 magnon에 대한 confinement poential이며, $\epsilon_{n\vec{k}}$는 n-th band에 대한 magnon dispersion을 나타낸다. 위 방정식들은 전자의 준고전적 운동방정식과 매우 유사하며, 이를 바탕으로 비슷한 현상이 나타날 것을 추측할 수 있다. 하지만 한가지 차이는 magnon은 전하가 없다는 점이며 이로 인해 전기장을 통해 유도될 수 없다. 대신에, magnon wavepacket은 온도 gradient를 통해 유도 될 수 있다. 온도 gradient의 효과 또한 edge current picture를 이용하여 위의 준고전적운동방정식으로 기술할 수 있다.
샘플의 edge 부근에서, confining potential $U(\vec{r})$은 edge를 따라 anomalous velocity를 일으킨다. edge를 따라 흐르는 전체 전류는 edge current를 형성하며, 이는 모든 edge에 대해서 동일하다. (We note that, in contrast to edge modes in quantum Hall systems, this current is not confined at the edge of the sample, but it mixes with a bulk magnon current.)
이 전류는 이름에서 알 수 있듯이 순환전류 이므로, 알짜 transport는 존재하지 않는다. 이러한 edge current는 Bose distribution function을 통한 온도에 의존한다. 그러므로, 만약 온도 gradient가 존재한다면 edge current는 양쪽 사이드에서 동일하지 않으며, net transverse current를 생성한다. 결과적으로, thermal Hall effect(Righi-Leduc effect)를 도출해낸다.
Thermal Hall conductivity는 아래와 같이 얻을 수 있다.


위에서 $\rho = \rho(\epsilon_{n\vec{k}})$는 Bose distribution function이며, $\mathrm{Li}_2(z)$는 polylogarithm function이다.
Magnon의 thermal Hal leffect는 파이로클로르 강자성체 $\mathrm{Lu_2 V_2 O_7}$에서 측정됐으며, 위 방정식 $\kappa^{xy}$의 계싼 결과와 잘 들어맞는다. 게다가, Berry curvature는 파동성과 연관되기에, 이 이론은 또한 고전적 magnetostatic spin-wave system(대표적으로 YIG)에도 적용시킬 수 있다. YIG 박막에서는, demag field가 spin-wave spectrum의 anisotropy를 만들어내는데, 이는 spin과 orbital motion 사이의 coupling을 야기한다. 이는 nonzero Berry curvature를 유도하며, 결과적으로 magnon의 thermal Hall effect와 edge current를 만들어낸다. YIG에서의 spin-wave transport에 대한 여러 연구들이 진행됐는데, 이는 긴 coherence length와 이를 스핀트로닉스 응용에 사용할 가능성 때문이었다. Spin wave의 wavepacket은 광학적으로 관측이 되며, coherence length는 cm 수준까지도 높아질 수 있다. 그러므로, YIG는 $\vec{k}$-space Berry curvature로 부터 나타나는 wave packets 동역학을 관측하는데 좋은 물질이 될 수 있을 것이다.
B.4. Valley-Hall effec in graphene
$\vec{k}$-space 에서의 Berry curvature는 또한 그래핀에서도 발생한다. 우리는 그래핀 단일층 에서의 sublattice asymmetry(다시 말해, A와 B sublattice 사이트에서 에너지적으로 다른 것)를 고려하고자 한다. 이는 pseudospin space에서 Zeeman-like 항을 추가하는 것으로 나타낼 수 있다.

여기서 $\vec{B}(\vec{p})=(p_x,\xi p_y, 0)$는 ($K\;(K')$) valley 속 Dirac carrier에 대한 low energy Hamiltonian 에서의 effective pseudospin field 이며 $U(-U)$는 A(B) sublattice에서의 electrostatic energy이다. 그러므로, Berry curvature는 아래와 같이 유도된다는 것을 예측할 수 있다.

위 방정식에서의 밸리 의존성은, 서로 반대되는 밸리 속에 있는 전자들이, 전기장이 인가됐을 때 분리된다는 것을 의미하며, valley-Hall effect라는 결과로 나타난다. 특히, 두 밸리에서의 전자 분포가 불균형한 경우, 0이 아닌 Hall voltage가 예측된다. 이는 valley filter등을 통해 실현 될 수 있을 것이다.
B.5. Topological insulators
Berry curvature 구조는 topological insulator(TI)에서도 존재한다. 잠시 TI에 대해 간단히 설명하고 넘어가자면, TI는 최근들어 각광받는 물질로, 물리적인 성질이나 미래 응용 가치로 인해 매우 관심을 끄는 물질이다. TI의 첫번째 예는 1980년 QHE에서 발견 됐다. 일반적인 부도체와 비슷하게, bulk quantum Hall state는 energy gap이 존재하며 non-conducting하다. 하지만 샘플의 엣지에서는, quantum Hall state가 electronic transport를 서포트하며, 주목할 만한 특징을 갖는다: 우선 그들은 chiral 하며(각 edge를 따라 확실한 방향으로 횡단한다), gapless 하며(bulk gap에 놓여있는 모든 Fermi energy에 대해 edge state가 존재한다), edge의 기하학 또는 disorder의 존재에 대해 매우 견고하다.
Quantum Hall conductance (QHC)는 Chern integer $n$이라 불리는 topological index로 나타낼 수 있는데, 이 $n$은 시스템의 연속적인 deformation에 대해 invariant하다. 이는 QHE state에 위상학적으로 non-trivial clasification을 갖게끔 한다.(일반적인 band insulator에서는, index $n$은 사라진다). 최근까지, 모든 topologically non-trivial insulator는 내재적으로 TR-breaking을 수반하는 것으로 생각되어 왔다. It was only until after the discovery of graphene that the TR-symmetric topologically nontrivial insulating phase was discovered.
2006년에, Kane과 Mele는 그래핀 내에서 SOC가 고려 될 때, 전자들이 마치 QHE에 대한 두개의 시간-반전 복제품(겹겹이 쌓인) 것 처럼 행동한다는 것을 제아했다. 이 경우, edge states가 쌍으로 존재하는 것으로, 서로 반대 부호의 스핀을 갖는 전자들이 각 edge를 따라 서로 반대방향으로 횡단하는 경우를 생각 할 수 있다(이 경우 helical하다고 한다). 이때 그들은 gapless하며 non-magnetic impurities에 의한 backscattering에 대해 매우 견고하다(왜냐하면 backscattering은 spin이 반전되는 경우에만 허용되기 때문이다).
앞서 말했듯이, 비슷한 이론적 제안은 Bernevig과 Zhang에 의해 strained semiconductor에서 이미 나온바 있다. 이 2차원 효과는 quantum spin-Hall effect (QSHE)라 한다. 2D QSHE는 HgTe quantum well 구조에서 발생하는 것으로 제안 됐는데, 이는 transport measurement로 이미 증명됐다. QSHE시스템인 HgTe 양자 우물에서는, 측정된 conductance가 $2e^2/h$의 값을 갖는데, 이는 두개의 완벽하게 conducting한 channel이 edge states를 따라 존재한다는 것에 대한 직접적인 증거이다.
2D QSHE는 Fu와 Kane에 의해 3D system으로 확장됐다. 3D TI에서는, spin-filtered surface states가 edge sates에 반대하여 나타난다. 이는 QHE와 닮은 점이 없다. 낮은 에너지에서는, surface states는 2D Dirac cone을 형성한다(i.e. 그들은 질량이 없는 Dirac fermiion이며, 아래와 같은 graphene-like Hamiltonian의 지배를 받는다. 그래핀이 두개의 valley를 갖는 것과 반대로, 한개의 valley만을 갖는다)
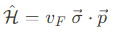
또한, 위 식에서 그래핀과는 반대로, $\vec{\sigma}$는 실제 spin을 나타낸다. 이 dispersion은 여러 시스템에서 관측 됐는데, 대표적으로 $Bi_2 Se_3$ 등이 있다.
In TI’s, a finite Berry curvature can result if only a gap
is introduced in the Dirac spectrum. Lu et al.127 considered
ultra thin topological insulator films and found that tunneling
processes between the top and bottom surfaces open up a
gap in the energy spectrum (the energy gap is proportional to
1=L2, where L is the film thickness). The corresponding
~k
-space Berry curvature was shown to result in a finite spin-
Hall effect at the TI surface, which will lead to an observed
spin accumulation at the edges.89 Alternatively, the ordinary
TI surface states in the presence of an exchange field due to
a deposited FM film also gaps the spectrum, and we expect a
finite Berry curvature. Moreover, in this scheme, the Berry
curvature should carry an explicit dependence on the gap
size, which is proportional to the FM magnetization; this follows
from an analogous situation in graphene when one
breaks sublattice asymmetry, giving rise to a Berry curvature
and the valley Hall effect.122 Having a tunable Berry curvature
is desirable from the point of view of tunable electronic
(topological) transport, most notably, the Hall effect.
C. Hall conductiviy
우리는 이 장에서 아래와 같은 일반적인 spin-orbit Hamiltonian의 Hall conductivity를 Kubo method를 이용해 유도하고 이 값이 본질적으로 $\vec{k}$-space Berry curvature와 연결되어 있음을 보이고자 한다.

정의에 따르면, single-particle retarded Green's function은 아래와 같이 주어진다.

위 함수에, 일반적인 spin-orbit Hamiltonian을 대입하면,

여기서 $\epsilon_\pm$과 $P_\pm$은 각각 아래와 같다.
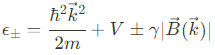
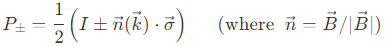
Kubo formula 공식을 이용한 Hall conductivity는 아래와 같다.
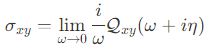
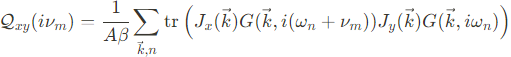
위에서 $A$는 system의 면적이고, $\omega_n$은 fermionic Matsubara frequency, 그리고 $\nu_m$은 bosonic Matsubara frequency이다. 위에서 구한 retarded Green's function을 위의 식에 대입하면,
... 중략
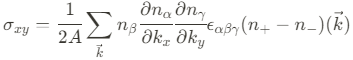
위 식을 first Brillouin zone (FBZ)에서의 integral로 변환하고, Fermi energy가 upper bands와 lower bands 사이에 있다고 가정하면,
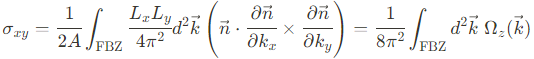
이 결과를 통해, 우리는 Hall conductivity가 $\vec{k}$-space Berry curvature를 FBZ에서 적분한 형태 임을 알았다. (물론 여기에는 Fermi energy가 energy gap 사이에 있다는 가정이 포함되어 있다.)
Spin-Hall effect의 경우, Berry curvaure는 spin-dependence를 유발한다. ($\Omega_z^\uparrow(\vec{k})=- \Omega_z^\downarrow(\vec{k})$). 이 효과로 인해 up-spin과 down-spin에는 각각 같은 양이면서 동시에 서로 반대 부호의 Hall conductivity가 주어지며, spin-Hall conductivity가 다음과 같음을 생각할 수 있다.
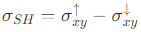
Time-reversal symmetry가 보존되는 시스템(예를 들어 자기장이 가해지지 않은 SOC 환경)에서는, 결과적인 spin-Hall conductivity가 수직방향의 pure spin current를 나타내며, 이때 up spin과 down spin의 캐리어들이 서로 반대방향으로 흐를 때 각 캐리어의 수는 동일하다. 이때 알짜 charge Hall conductivity $\sigma_{C,xy}= \sigma_{xy}^\uparrow+ \sigma_{xy}^\downarrow$는 상쇄된다. 그러므로, TR symmetric SOC system는 pure spin current 소스로서 좋은 후보군이 될 수 있다.
시스템 속 Fermi level이 gap 사이에 존재하여, 모든 밴드들이 완전히 채워졌거나 비워진 상태에서는, $\sigma_{xy}$는 위상적으로 invariant하다. 만약 $\vec{n}(\vec{k}):\;T^2\longrightarrowS^2$을 2차원 FBZ에서 unit sphere로의 맵피으로 본다면, integral $\vec{n}\cdot\partial_k_{x} \vec{n}\times \partial_k_{y} \vec{n}$은 위상적으로 $4 \pi n$의 값을 가지며 양자화 되며, $n \in Z$는 $\vec{n}$의 winding number이다.
위에서 $\vec{k}$-space Berry curvature의 항으로 만들어진 Hall conductivity $\sigma_{xy}$는 quantum Hall effect (QHE)에도 적용할 수 있는데, 이 경우는 강한 외부자기장이 존재할 때 나타난다. 이 경우에는, integer n은 TKNN index로서 알려져 있으며, 물리적으로는 Fermi level 밑에서 채워져 있는 Landay level의 수를 알려준다. 특히, 비록 Landau-level 문제가 일반적인 SOC 문제와는 매우 다르지만, Hall conductivity의 topological quantization은 두 경우 모두 공통적인 $\vec{k}$-space Berry phase effects에서 나타난다.
실제로, QHE에서의 $\vec{k}$-space Berry curvature는 lattice가 가지는 주기성으로 정의된 Bloch wavefunction $ | u_n(\vec{k}) \rangle$이 $\vec{k}$에 대해 adiabatically evolve 할 때 발생한다. 후자는 또한 극저온에서의 anomalous Hall effect의 intrinsic contribution에도 영향을 끼친다.
'책 정리 > Gauge Fields in Spintronics, T. Fujuta' 카테고리의 다른 글
| II. SPIN-1/2 SYSTEMS IN THE PRESENCE OF SPATIALLY VARYING MAGNETIC FIELDTEXTURES (0) | 2023.12.06 |
|---|---|
| III. REAL SPACE GAUGE FIELDS IN GRAPHENE (0) | 2023.12.06 |
| IV. SPIN-ORBIT COUPLING SYSTEMS: REALSPACE ANALYSIS (0) | 2023.12.06 |
| VI. TIME-DEPENDENT MAGNETIC SYSTEMS (0) | 2023.12.06 |
| VII. Summary (0) | 2023.12.06 |
댓글