앞의 4개의 섹션에서, 우리는 real-space와 momentum-space의 gauge fields의 근원과 그들의 물리적 결과들을 다루었다. 우리는 다음으로 또 다른 차원에서의(시간을 추가한) gague fields에 대해 다룰 것이다. time-space 에서의 gauge fields는 뒤에서 볼 것이지만, 스핀트로닉스 시스템에 있어서 매우 중요한 물리적 결과들을 포함하고 있다. 우리는 아래에서 그들을 볼 것이다.
A. Derivation
Time-space에서의 gauge field는 시변 자기장 $\vec{B}(t)$가 존재하는 spintronic systems에서 자연적으로 발생한다. 이 시스템에서의 Hamiltonian은 아래와 같은 형태를 갖는다.

앞전 섹션에서 했던 방법을 따라, 우리는 Schrodinger equation $\hat{\mathcal{H}}|\psi \rangle = \epsilon |\psi \rangle$을 시간 t에서, Unitray transformation $U(t)$를 적용하여 대각화 할 것이다.
Energy operator를 시간미분 꼴 $\epsilon = i \partial_t$를 적용하면, 우리는 아래와 같은 결과를 얻는다.

우항에서, 우리는 $U$의 time-dependence로 부터 time-space 속 gauge field를 구했다.
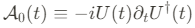
이 gauge field의 물리적 의미를 끄집어내기 위해, ...
728x90
'책 정리 > Gauge Fields in Spintronics, T. Fujuta' 카테고리의 다른 글
| II. SPIN-1/2 SYSTEMS IN THE PRESENCE OF SPATIALLY VARYING MAGNETIC FIELDTEXTURES (0) | 2023.12.06 |
|---|---|
| III. REAL SPACE GAUGE FIELDS IN GRAPHENE (0) | 2023.12.06 |
| IV. SPIN-ORBIT COUPLING SYSTEMS: REALSPACE ANALYSIS (0) | 2023.12.06 |
| V. SPIN-ORBIT COUPLING SYSTEMS: k-SPACE ANALYSIS (0) | 2023.12.06 |
| VII. Summary (0) | 2023.12.06 |



댓글