Green's function method는 특정 미분방정식(전자기학에서의 inhomogeneous Maxwell equation 등..)을 푸는데 매우 유용하다. 양자장론에서, Green's function method 시스템의 다이나믹스를 분석하는데 사용된다. 이 글에서, 우리는 우선 fermion에 대한 one-particle Green's function부터 시작하고자 하며, Green's function에 대한 analyrical properties를 소개하고자 한다. 더욱이, 우리는 0K 에서의 Green's function, 즉 Matsubara Green's function에 대해서 다룰 것이다.
2.1.1. Green's function for free electron gas
맨 처음, 우리는 electron Green's function의 특성에 대해 알아보기 위해 free electron gas를 묘사하는 단순한 Hamiltonian 부터 시작할 것이다. Second quantization에서의 free electron gas Hamiltonian은 아래와 같다.
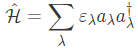
여기서 $\varepsilon_\lambda$는 $\lambda$ state의 eigenenergy이며, 전자의 momentum과 spin space를 특정시킨다. $a_\lambda^\dagger$, $a_\lambda$는 fermion의 creation, annihilation opeator이다.
Electron Green's function은 아래와 같이 정의된다.

여기서 $|0\rangle$은 vacuum state이며, $a_\lambda^\dagger(t)$, $a_\lambda(t)$는 Heisenberg picture에서의 creation, annihilation operator이다.

위의 식에서는 아래와 같은 commutation relation을 이용했다.
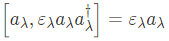
Time ordering operator $\hat{\mathcal{T}}$는 시간 구간에 따라 아래와 같이 explicitly 하게 나타낼 수 있다.

보이듯이, anti-causal case ($t \ll t'$)의 경우, Green's function은 양의 부호를 가지며, 이는 fermion operator들의 anti-commutation relation 때문이다. Bosong의 경우, 이는 반드시 음의 부호를 가져야 한다.
Heisenberg picture에서의 creation, annihilation operator를 electron Green's function으로 대체하면,
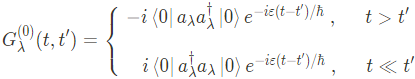
여기서 $\langle0| a_\lambda^\dagger a_\lambda|0\rangle$은 state $\lambda$의 particle number이며 zero-temperature Fermi distribution function $f(\varepsilon_lambda)$로 볼 수 있다. 이를 이용해 다시 Green's function을 쓰면

위 식에서 우리는 electron Green's function을 $G_\lambda^{(0)}(t-t')$을 다시 썼으며, 이는 Green's function이 명백히 시간에 대해 homogeneous하기 때문이다. 이 Green's function을 Fourier transformation을 하면,
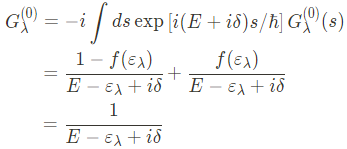
위 식에서 infinitesimal damping 항 $i\delta$는 Fourier integral을 converge 하기 위해 사용 됐으며, 아래와 같이 정의된다.
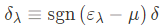
Green's function $G_\lambda^{(0)}$을 얻는 또 다른 방법은, $G_\lambda^{(0)}(t,t')$의 equation of motion을고려함으로써 얻을 수 있다. 시간에 대해 homogeneous인 시스템을 고려해보자, $\tau \equiv t-t'$라 정의하면, 위의 식은 아래와 같이 쓸 수 있다.
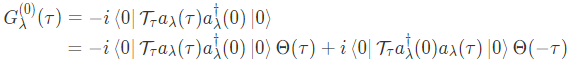
여기서 $\mathcal{\Theta}$ function은 아래와 같다.
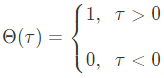
위의 $G_\lambda^{(0)}(\tau)$식을 시간 $\tau에 대해 미분하면, Green's function의 equation of motion은 아래와 같다.
'Other Topics' 카테고리의 다른 글
| Orbital Angular Position (0) | 2024.03.27 |
|---|---|
| First Principles Calculation (0) | 2023.10.31 |
| (작성중) Linear Response Theory (0) | 2023.10.31 |
| 양자얽힘 (Density Operator로 보는 Quantum Entanglement) (0) | 2023.08.23 |
| 4f orbital electrons (0) | 2023.08.17 |



댓글