참고문헌
[1] 양자얽힘, KAIST 문은국 교수님
Single Qubit의 양자역학
Single qubit은 두개의 basis로 complete set을 구성한다. 다시 말해 dimension은 2이다. 이를 state term으로 나타내면 다음과 같다.

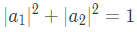
여기서, observable로서의 의미는 없지만, quantum entanglement의 여부를 알기 위해서 필요한 'density operator'를 정의해보고자 한다.
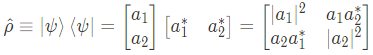
이 density operator의 특징으로는, 자기 자신의 곱셈이 자신과 같다는 것이다. 이를 실제로 곱해보자.

또한 특정 Hamiltonian의 평균 값을 구하는 경우, 아래와 같은 성질도 성립한다.
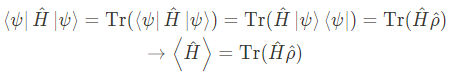
이제 double qubits로 넘어가겠다. double qubits는 4개의 basis로 complete set을 구성하며, 4 dimension을 갖는다. single qubit처럼 state로 나타내면 다음과 같다.

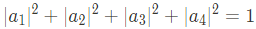
이 double qubits 상태에서, EPR state는 다음과 같이 작성할 수 있을 것이다.
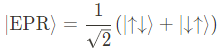
또한 polarized state는 다음과 같을 것이다.
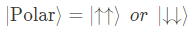
이제 위에서 말한 것처럼, quantum entanglement의 여부를 'density operator' 통해 알아보고자 한다.
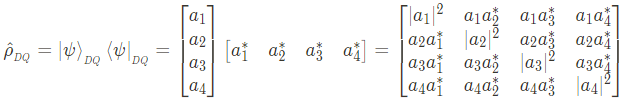
How do we know about entanglement? : Using reduced density operator!
두 paritcle중 하나의 정보를 없애버리면 4x4 $\rightarrow$ 2x2 matrix로 변한다.
어떻게? 바로 아래 식을 이용하면 된다.

EPR State에 대해서 density operator를 구하면

$\hat{\rho}_{_{EPR}}$을 위의 $\hat{\rho}_{_{DQ}}$에 대입하면,
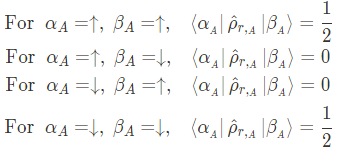
That is, we can write
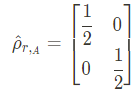
이 reduced density operator에서는, 자기 자신과의 곱이 자기 자신이 되지 않는다. 다시 말해, entangled 되어있다고 볼 수 있다. (왜냐하면 entangled 안된게 자기자신과의 곱이 자기자신이 됐으므로!)
* Product state는 대부분이 entangled되어있지 않다. 다시 말해, Fully polarized state는 entangled 되어있지 않다. 다 시 말 해, FM은 entangled 되어있지 않다.
'Other Topics' 카테고리의 다른 글
| (작성중) The Green's Function Method (0) | 2023.10.31 |
|---|---|
| (작성중) Linear Response Theory (0) | 2023.10.31 |
| 4f orbital electrons (0) | 2023.08.17 |
| Exchange Stiffness Constants (0) | 2023.08.17 |
| Avoided Crossing (0) | 2023.07.17 |




댓글