참고 문헌
[1] 曲冠雄, 強磁性体におけるスピンホール効果
1. The Kubo formula
Linear response theory는 섭동 외력에 대해 observable의 linear order response를 공식화 한 것이다. 예를 들어, conductivity는 외부 전기장에 대한 전류의 linear response라 할 수 있을 것이다. Linear response approximation은 일반적인 non-equilibrium 조건과 비교할 때 매우 단순화 과정을 거친다. 이는 linear response가 시스템의 equilibrium 특성에 의해 uniquely 결정되기 때문이다.
우선 정적인 파트와 perturbation의 합으로 구성된 일반적인 Hamiltonian을 고려해보자.

여기서 ˆH0는 perturbation이 없는 경우의 시스템(Hamiltonian)을 나타내고, ˆH′(t)는 시변 Hamiltonian으로 여기서 t가 perturbation이라 볼 수 있다.
Non-equilibrium state에서는, 임의의 observable ˆA의 expectation value는 아래와 같이 time-depenent하다.

여기서 ˆρ(t)는 시간에 따라 변화하는 density operator이다. Density operator의 time evolution은 time evolution operator에 의해 지배된다.

여기서 ˆρ′(t)≡ˆρ0 는 initial time (equilibrium state)에서의 density operator로 정의되고, 또한 time-dependent Hamiltonian의 time evolution operator는 아래와 같다.

여기서 T는 time-ordering operator이다.
+) Density matrix operator는 Heisenberg picture에서는 시간에 따라 변화하지는 않지만, Schrodinger picture에서는 변화함을 인지하자. 이는 matrix form으로 쓰면 더 명확해진다.

Time evolution operator에 포함되어 있는 time-ordering operator는 analytically 계산하는데 있어 번거롭지만, interaction picture에서는 이를 ˆH′의 order로 전개 시킬 수 있다. 이는 Hamiltonian의 time-dependent 부분이 perturbative하기 때문이다.
1차 항의 경우, 우리는 아래와 같이 쓸 수 있다.

여기서 tr은 reference time이다.
결과적으로, time evolved density operator는 ˆH′의 1차식으로 전개시킬 수 있다.

여기서 reference time을 tr=t′=−∞라 가정하면, 외력은 부재하게 되며, system은 equilibrium state $\hat{\rho}_0에 머무르게 된다.

위 방정식은 $\hat{\mathcal{H}'_I$ 속에서 외력이 작용할 때의 density response라 할수 있다.
결과적으로, 외력이 작용할 때 물리적 observable ˆA의 exepctation value는 다음과 같다.
'Other Topics' 카테고리의 다른 글
| First Principles Calculation (0) | 2023.10.31 |
|---|---|
| (작성중) The Green's Function Method (0) | 2023.10.31 |
| 양자얽힘 (Density Operator로 보는 Quantum Entanglement) (0) | 2023.08.23 |
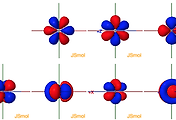
| 4f orbital electrons (0) | 2023.08.17 |
| Exchange Stiffness Constants (0) | 2023.08.17 |
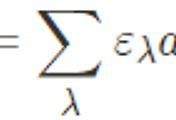
댓글