수소원자에서는, Coulomb force에 더해 electron-electron repulsion을 고려해야 한다. 이 두 힘은 order of magnitude가 비슷하기에 perturbation을 원래 쓰면 안된다. 하지만 한번만 perturbation으로 가정하고, energy correction을 구해보고자 한다.


이때 $/phi$ 함수는 아래와 같으므로,
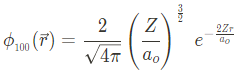
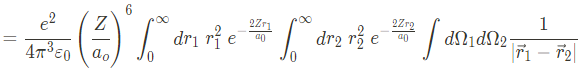
위 식에서 angular part를 잠깐 보면
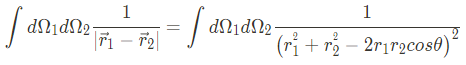
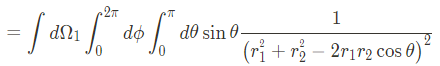
여기서 $ r_{1}^{2}+r_{2}^{2}-2r_1r_2cos\theta \equiv t $로 놓으면 아래와 같이 치환 시킬 수 있다.


이 경우 energy shift는 아래와 같다.

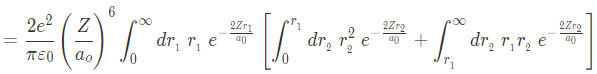

수소 원자의 경우 Z=2 이므로, $\Delta E \sim 34eV $이고, 그러므로 최종적인 E는 약 -74.8eV이다. 이는 실제 값 -78.975eV와 약 4eV 정도 차이가 난다. 이 차이는 electron들이 서로 proton을 screening 해주는 효과로 인한 것이다.
이제 first-excited state에 대해서도 같은 계산을 반복하자.

여기서 u의 함수는 다음과 같다.
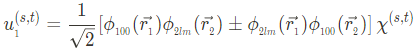
Then,


여기서 위의 항은 direct term $J_{nl} > 0$이며, 아래항이 exchange term $K_{nl} > 0$이다. 이때 exchange term은 고전적으로 이해할 수 있는 양이 아니다. Identical Fermion의 total wavefunction을 antisymmetric하게 만들기 위해서 나온 term으로서, purely quantum mechanical component이다.
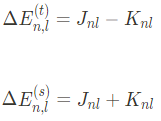
다시 exchange term을 보면, Coloum interfaction, electric repulsion으로 시작한다 (spin과 무관)
하지만 결과는 spin dependent하다 ( Spartial aprt가 antisym/sym 이냐에 따라서 spin이 singlet이냐, triplet이냐가 결정되기 때문)
'책 정리 > 양자역학 (송희성)' 카테고리의 다른 글
| 13.3) (0) | 2023.06.05 |
|---|---|
| 12.1) Relativistic correction & spin-orbit correction (0) | 2023.06.02 |
| 16.1) Aharonov-Bohm effect (0) | 2023.06.01 |
| 16.3) The constant magnetic field (0) | 2023.06.01 |
| 12.3) The anomalous Zeeman effect (0) | 2023.05.29 |




댓글