Linearity = ease of use and predictability.
Nonlinearity = uncertainty and with a lack of ease
Simply put, nonlinearity refers to a relationship that cannot be modelled or explained asa linear algebraic or differential combination of input or state variables. onlinear systems differ completelyfrom linear systems.
The behaviour of a nonlinear system can be sensitive to the parametersof the systems and the initial conditions of the system.
A chaotic system contains an infinite number of differentperiodic orbits, which are dense in the state space of the system.
But, nature is non-linear! (Transistor, 등등..)
In a nutshell, a nonlinear system can be considered to be a complex library of different behaviours.
특징
It was proposed in 1998 that chaotic systems might be utilized to design computing devices (by Ditto)
Chaos computing is based on the nonlinear dynamical principles and can perform all logical operations
* Reuse of logic morphable gates
A system is capable of serving as a universal general purpose computing provided it can emulate all logic gates. Using single chaotic element, each logical operation (AND, OR, NOT, NAND, NOR, XOR, ) can be realized. Computer memory can be constructed by combining logical gates. -> A completely different circuit could be implemented on the same hardware.
Chaos computing may also lead to dynamic architecture, where the hardware design itself evolves during the course of computation. (chaotic systems can be made to produce all types of logic gates and further allow them to be morphed into each other.)
Chaos computing is a new unconventional paradigm for computing, where chaotic oscillators are used for computation.
In mathematics, chaos signifies that the equations expressing nonlinear systems are extremely sensitive to initial inputs or conditions and it is hardly possible to predict their future behavior with a high degree of certainty.
Chaos has three defining characteristics
(1) sensitivity to initial conditions,
(2) aperiodic long-term behavior, and (3) it is wholly deterministic.
The dynamic chaotic computer can perform computations and is promising because of its flexibility for changing logic gates by slightly modifying its parameter values.
Chaotic computer can directly perform basic numerical operations like addition and multiplication.
A chaotic system enables us to build better computers that have a flexible instruction set and carry out computation that conventional computers are not good at.
Chaos represents a deterministic dynamical system that is nonlinear, sensitive to initial conditions (the so-called butterfly effect), and exhibits sustained irregularity.

Pros
Low power and high speed. Reconfigurable or dynamic logical architecture. A universal form of general-purpose computing
Cons
The term “chaos computing” was popularized by William Ditto of the Georgia Institute of Technology, who believes that the unpredictabilty of chaotic processes may power a new breed of computer. Ditto's chip is like the microelectronic version of a stem cell that can assume all sorts of different functions.
Choas computing takes advantage of the richness of nonlinear dynamical systems and insights from neural systems to devise new approaches to create a chaos-based computer. Nonlinear dynamics has revealed a rich array of behaviors, especially those related to chaos including routes to chaos, high and low dimensional chaotic attractors, and transient chaos. In neural systems, measured phenomena include chaos, synchrony, and cascading avalanches demonstrating that information processing in the brain is not just anatomical, but also dynamical.
Examples


Chaos computing can be applied for generic computation, DNA computing, modeling speech, and speech processing. It can also be implemented in specialized domains such as a biological environment and nano fluidics.
III. BENEFITS AND CHALLENGES
Chaos based architectures can help us avoid trillion dollar research and development that has only marginal gains.
Novel chaos computing can lead to new paradigms for the optimization of solving complex problems, such as controllers for autonomous systems, including robots and vehicles. A number of challenges may hinder the development of practical chaos-based computers. One major challenge for developing chaos-based computers is that the overhead associated with the physical implementation of a chaotic gate is quite higher than an equivalent digital gate [8].
IV. CONCLUSION
2.1. Dynamical System
Dynamical system은 시스템 속에 있는 초기 state로부터, 해당 state의 time evolution을 기술하는 방정식으로 묘사되는 시스템이다. 이 방정식들은 시스템 속에서 시간에 연속적인 evolution을 나타낸다.
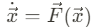
여기서 $\vec{x}$는 system 속의 state vector이다. 이때 방정식은 이산적인 시간 evolution을 기술하는 꼴로도 나타날 수 있으며, 이 때 방정식은 아래와 같다.

여기서 $\vec{x}_k$는 시스템 속에서 time step 'k'에 있는 state를 나타낸다. States의 순서는 시스템 속에서 state vector space의 궤도를 그린다.
맥스웰의 플라즈마 방정식, 나비에-스토크스 유체 방정식, 뉴턴 운동 방정식은 모두 dynamical system의 예제이다.
Dynamical equation은 linear 할 수도 있고, non-linear 할 수도 있다. 각각의 경우에, 시스템의 state vector를 구성하는 변수는 state space를 span해야 한다. 이는 다시 말해, 그들은 반드시 시스템의 현재 상태를 묘사할 수 있어야 한다. 결과적으로, 시스템의 미래 상태 또한 완벽하게 묘사할 수 있게 된다.
2.1.1. Linear Dynamical System
Linear dynamical system은 동역학 방정식이 linear한 시스템이다. 다시 말해, 시스템의 특성(위치, 속도, 가속도, 전류, 전압 등...)를 묘사하는 dynamical variables는 방정식 속에서 linear 한 항으로 나타난다.
Linear system은 2개의 파트로 나눠질 수 있으며, 각각의 파트는 분리되어 계산 할 수 있고, 추후에 이 솔루션들은 재결합되어 linear system의 해답을 구할 수 있다. 이 reduction은 복잡한 시스템을 단순화시키는데 큰 도움이 된다.
라플라스 변환, 푸리에 변환, 그리고 superposition argument는 are examples of the application of such simplifications in a linear system, where the system is described and solved in terms of a basis set of simple solutions.
Linear dynamical system이 가지는 이점 중 하나는, one can solve it and obtain a closed-form equation for its time evolution.
Having such a closedform solution for the linear dynamical system implies that knowing the initial condition of the system results in full knowledge about its entire future evolution.
그저 시스템의 closed form solution에 initial condition을 넣으면, 미래 어느 순간의 시스템의 정확한 state를 알려줄 것이다.
The main idea behind Von Neumann architecture is to define a set of basic instructions that can encode any problem (an instruction set) and then implement these fundamental instructions within the hardware. Then for any problem one can write a program, which consists of instructions from this instruction set, and then feed this program along with the corresponding data inputs to the computer. The computer reads this program and executes it line by line. Execution of an instruction is nothing more than sending the appropriate
https://journals.aps.org/prl/pdf/10.1103/PhysRevLett.81.2156
Irregular behaviors include the weather, stock markets, casino games, and so forth. However, while regular behavior repeats a single pattern or multiple patterns in a predictable and unchanging manner, irregular behaviors (usually attributable to nonlinear effects, thus the name nonlinear dynamics) are much more varied and includes two extremes: random dynamics and chaotic dynamics.
The distinctive feature of this alternative computing paradigm was that it exploited the sensitivity and pattern formation features of chaotic systems.
exploit a single chaotic element to reconfigure into different logic gates through a threshold-based morphing mechanism
to use the rich temporal patterns embedded in a nonlinear time series in a controlled manner to obtain a computing device that is flexible and reconfigurable.
General Concept
우리는 아래서 한개의 nonlinear system을 이용하여 기초적인 logic gate를 얻는 이론적인 방법을 가볍게 훑고자 한다. 여기서의 개략적인 목표는 nonlinear time series에 내재된 풍부한 temporal patterns들을 우리의 목적에 맞게 사용하여 호환성이 높고 재구성이 가능한 컴퓨팅 소자를 얻는 것이다.
state가 x라는 값을 통해 represent 되는 chaotic element(chaotic chip, 또는 chaotic processor)를 고려해보자. 우리의 scheme에서, 모든 기본 logic gate operation은 아래의 step들을 포함한다.
1) Inputs :
$ x \rightarrow x_0 +X_1 +X_2$ for 2-input logic operations. (NAND, NOR, XOR, AND, OR, and XNOR)
$ x \rightarrow x_0 +X$ for 1-input operations. (NOT)
여기서 $x_0$는 시스템의 initial state이고, $ I = 0$일 때 $X=0$이다.
만약 $ I =1 $이라면, $X = V_{in}$이 되고, 이때 $V_{in}$은 양의 상수이다.
2) Dynamical update
state가 x에서 update 되어 f(x)가 됨 ( 여기서 f(x)가 nonlinear function이다)
3) Threshold mechanism to optain outupt Z:
Z = 0 if f(x) <= E,
Z = f(x)-E if f(x) > E
여기서 E는 monitoring threshol이다.
이는 logic gate의 관점에서 Z = 0일때 output 도 0, 그리고 Z>0일때 ($Z~V_{in}$) output 은 1은 내놓는 것으로 해석된다.
시스템이 non-linear하기 때문에, $x_0$을 정확히 명시하기 위하여 컨트롤 메커니즘이 필요하다. 우리는 여기서 $x_0$을 세팅하기 위해 threshold controller를 도입할 것이다.
다시 말해, 우리는 threshold controller의 clipping action을 사용하여 initialization과 더 나아가 output을 얻는 것을 진행할 것이다. 우리의 implementation에서는, input과 output이 동등한 정의를 가짐을 요구한다 , as well as among various logical operations. This requires that constant V_{in} assumes the same value throughout a network, and this will allow the output of one gate element to couple easily to another gate element as input, so that gates can be wired directly into gate arrays implementing compounded logic operations.
Chaotic systems generate large numbers of patterns of behavior and are irregular because they switch between these patterns. They exhibit sensitivity to initial conditions which, in practice, means that chaotic systems can switch between patterns extremely fast.
Modern digital computers perform computations based upon digital logic operations implemented at the lowest level as logic gates. There are essentially seven basic logic functions implemented as logic gates: AND, OR, NOT, NAND, NOR, XOR and XNOR.
A chaotic morphing logic gate consists of a generic nonlinear circuit that exhibits chaotic dynamics producing various patterns. A control mechanism is used to select patterns that correspond to different logic gates. The sensitivity to initial conditions is used to switch between different patterns extremely fast (well under a computer clock cycle).
As an example of how chaotic morphing works, consider a generic chaotic system known as the logistic map. This nonlinear map is very well studied for its chaotic behavior and its functional representation is given by:

In this case, the value of x is chaotic when r >~ 3.57... and rapidly switches between different patterns in the value of x as one iterates the value of n. A simple threshold controller can control or direct the chaotic map or system to produce one of many patterns. The controller basically sets a threshold on the map such that if the iteration ("chaotic update") of the map takes on a value of x that lies above a given threshold value, x*, then the output corresponds to a 1, otherwise it corresponds to a 0. One can then reverse engineer the chaotic map to establish a lookup table of thresholds that robustly produce any of the logic gate operations.[1][2][3] Since the system is chaotic, we can then switch between various gates ("patterns") exponentially fast.

"Chaos computing" isn't a widely recognized term in the field of computer science or technology as of my last update in January 2022. However, it might refer to a theoretical or emerging concept that involves harnessing chaotic systems or principles in computational processes.
Chaos theory deals with the study of complex systems that are highly sensitive to initial conditions, leading to seemingly random behavior over time. While chaos theory has applications in various fields such as physics, mathematics, and biology, its direct application in computing is less common.
In theory, chaotic systems could be utilized in computing for tasks like generating random numbers or optimizing algorithms. However, practical implementations and applications of chaos theory in computing are relatively limited compared to more established paradigms like deterministic algorithms or machine learning.
If "chaos computing" refers to a specific concept or development that has emerged since my last update, I'd recommend checking more recent sources or providing additional context for further discussion.
ㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡ
The main problems of modern digital computers are that (1) although the technology used for implementation can be extremely fast, the computation can remain relatively slow. The reason is that, in modern digital computers, instead of direct calculation of the problem a programmed version of the problem in terms of that computer’s instruction set of the computer is executed. Such programs are executed instruction by instruction, with each instruction initiated by a master clock. Each instruction takes one or more cycles (unless parallelism is available and feasible). (2) The second problem is that, although the computer is “programmable”, ironically the hardware is not programmable. As said before, for each instruction in the fundamental set of instructions, there is one physically separate hardware implementation, and, at the arrival of each instruction to be run, the corresponding hardware implementation of that instruction is used while the remainder of the hardware is idle. As a result, inside the hardware for a programmable digital computer, there are dozen of implementations for instructions, but at each cycle, just one of them is used. These unused implementations of instructions are just wasting power and chip area.
This architecture will use these chaos-based logic blocks to obtain a truly reconfigurable computer, in which the hardware of the computer is truly reprogrammable. Such a computer will utilize all of its resources, so there will be no waste of power or IC area. Furthermore, since the hardware itself is deeply reconfigurable, the programmability of the computer will not be restricted to just an instruction set, and the user will be able to program the computer to be an almost exact implementation of his application.
The main idea is to bridge the concepts between chaos theory and information processing systems, and find counterparts for each concept of information processing in chaos theory.
'Other Topics' 카테고리의 다른 글
| 대칭성과 대칭성 붕괴 (Symmetry and Symmetry Breaking) (1) | 2025.01.21 |
|---|---|
| Boltzmann Machine (0) | 2024.11.26 |
| Interfacial Spin Mixing Conductance (0) | 2024.04.01 |
| Orbital Angular Position (0) | 2024.03.27 |
| First Principles Calculation (0) | 2023.10.31 |



댓글