1.6The Rashba Effect
In a two-dimensional electronic system (2DES) with significant in-plane symmetry and broken out-of-plane symmetry, spin orbit coupling breaks the degeneracy between states with different spin, resulting in what is now known as the Rashba effect.34 With the addition of the Rashba term, the Hamiltonian for such a system is35

where λ is a constant that describes the strength of the Rashba coupling, me is the effective mass, and ^z is the normal unit vector. The schematic band structure is shown in Figure 1.5.
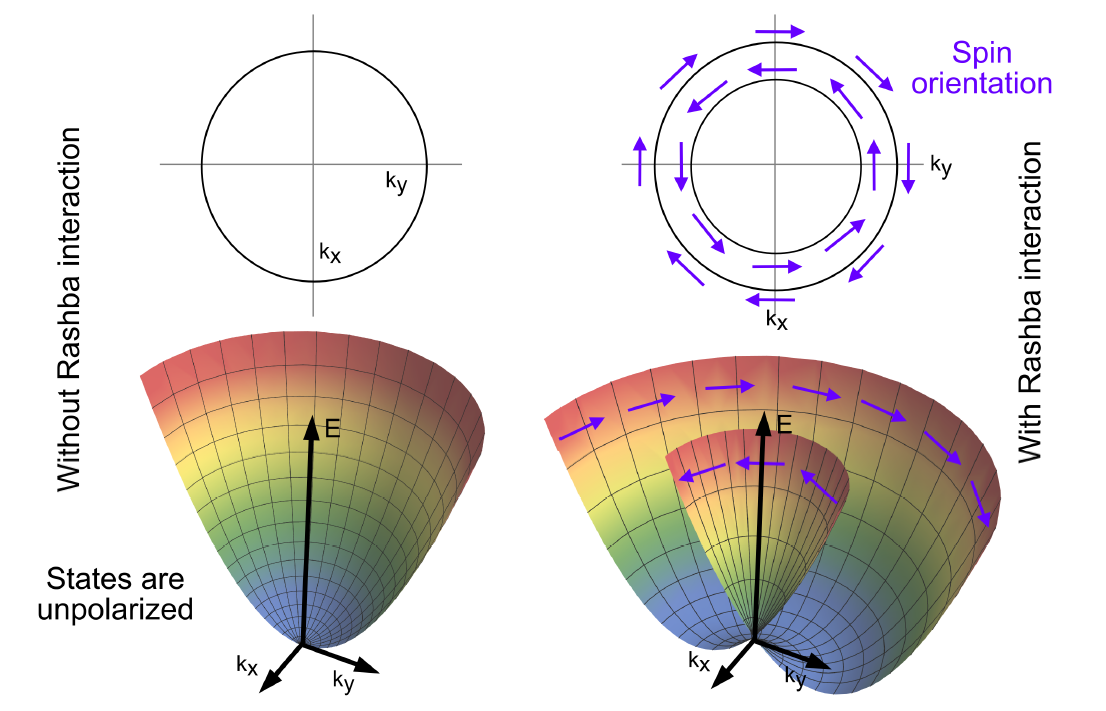
Figure 1.5. Schematic diagram of Rashba split surface states, after Krupin et al.36 The upper panels show a “top-down” diagram of the surface states at the Fermi level, while the lower two show a cross-section of the band structure for the two in-plane directions. The Rashba interaction breaks spin degeneracy in the Hamiltonian
Spin and momentum are coupled, and an electric current flowing in the plane will generate a spin polarization oriented perpendicular to the direction of the current. (The inverse is also true, and a spin accumulation can be used to generate a current).37,38 This effect can also occur in magnetic materials, where spin-orbit coupling adds a perturbation to the normally-uniform spin texture due to the exchange interaction.39
Spin accumulations generated via the Rashba effect can apply spin torques to adjacent magnetic layers (or the layer itself if magnetic).39 To first order, these generate a “field-like”, out-of-plane torque.40 These torques can occur in systems where the spin Hall effect also plays a role, which can lead to miss-identification of the primary source of the torques.30,31
Rashba coupling at metallic interfaces
Rigorous spin-orbit Hamiltonian은 전체의 전기적 포텐셜에 대한 상대론적 디락 방정식에 녹아져 있는 반면에, Rashba model과 같은 reduced spin-orbit Hamiltonian이 현실적으로 더 유용하다. 왜냐하면 고체 속 포텐셜의 일부분만 어림짐작하여 알려져 있기 때문이다. 더욱이, model Hamiltonian would make theoretical calculations analytically tractable.
Rashba coefficient에 대한 계산을 시작하기 위해, 대칭성이 깨진 포텐셜 $V(\vec{r})$을, 그리고 이에 더해 주기성을 가지며 electronic band를 결정하는 포텐셜 $V_p(\vec{r})$을 가정하자. 만약 $V(\vec{r})$을 Bloch electron의 perturbation이라 하면, Bloch electron의 에너지는 아래와 같다.

우리는 여기서 potential이 lattice constant scale에 비해 사앧적으로 느리게 변화한다고 가정하여, potential을 동적변수라기 보다는 parameter로 고려할 것이다. 이는 관점에 따라 $\vec{\nabla}V(\vec{r})$을 느리게 변화하는 전기장으로 볼 수도 있다.
그러므로, 두번째 항은 Bloch 전자에 대한 전기장의 dipolar interaction을 나타낸다. 단순히 따지면, band index $n$이 없어지게 된다. 이때의 position에 대한 expectation value는 알애ㅘ 같이 정의되며, 이때 $\psi_{\vec{k}\sigma}(\vec{r})$은 Bloch wavefunction이다.
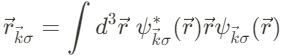
Bloch states는 아래와 같은 local Wannier orbitals (이때 Wannier function W_{\vec{R}}(\vec{r})은 lattice site $\vec{R}$에서의 atomic orbital의 linear combination으로 이루어진다)로부터 만들어 질 수 있다.
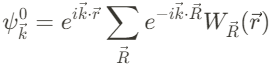
Atomic spin-orbit은 일반적으로 아래와 같이 모델링 되며, U는 atomic orbital의 potential이다.

이 경우, spin-orbit coupling을 perturbation으로 가정함으로써 Bloch wavefunction안에 spin-orbit coupling $\hat{\mathcal{H}_{so}$를 포함시킬 수 있게 된다.

To first order in the spin-orbit coupling, we have

여기서 Wannier function이 site $\vec{R}$에 대해 거의 구형임을 가정하면, 위의 방정식은 아래와 같이 축약된다.
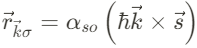
여기서 Rashba coupling coefficient는 아래와 같다.

위 공식에서는 isotropic assumption이 들어갔다. 위의 $\vec{r}$에 대한 방정식은 atomic SOC에 의해 발생하는 "side-jump"로 정의할 수 있다: $\vec{k}$의 momentum을 갖는 Bloch state가 wavepacket의 센터를 atom의 센터에 대해 사이드 쪽으로 바꿔버리는 것으로, 이는 Berger에 의해 제안된 anomalous Hall effect의 메커니즘을 설명하는데 도움이 된다.
만약 우리가 전도성 금속 물질의 spin-orbit energy $\Delta_{so}$를 수 eV라 한다면, side-jump는 어렴풋이 1옹스트롬 정도 될 것이며, Compton length $\lambda_c = \hbar/mc$의 크기보다 두~세배 오더 정도 크다.
위의 방정식을 Rashba Hamiltonian에 넣으면,

위의 Rashba Hamiltonian은 Pauli spin-orbit coupling에 의한 Hamiltonian $\hat{\mathcal{H}}_{pauli}=(\hbar \mu_B/2mc^2)(\vec{\nabla}V(\vec{r})\times\vec{p})\cdot\vec{s})$보다 수 오더 정도 차이가 난다. 이는 강력한 atomic spin-orbit coupling이 영향을 끼치는 enhancement factor 때문이다. 더 약한 summetry-breaking potential $V(\vec{r})$은 직접적으로 spin-orbi coupling을 제공하지는 않으며, atomic spin-orbit coupling에 의해 유도되는 dipole moment(또는 side jump)를 dipolar interaction을 이용하여 커플링 시킨다.
위 방정식에 interface potential ($V(\vec{r})=V(z)$fmf eodlqgkaus, 금속 계면에서의 Rashba spin-orbit coupling은 아래와 같이 쓸 수 있다.
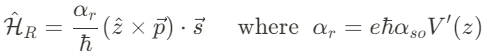
금속에서는, 계면 포텐셜 $V(z)$은 screened되며, $V'(z)$는 interface로부터 screening length 내에서만 0이 아닌 값을 갖는다. 위의 언급한 내용들은 정성적으로 spin-oribtal coupled band를 포함하는 물질에서 Rashba coupling의 존재를 support한다.
하지만 Rashba coefficient에 대한 정량적 해석은Kohn-Sham potential을 가지는 SOC를 포함하는 band structure를 정확히 계싼한다 한들 쉽지 않은 task이다. 이는 Rashba coupling이 microscopic Hamiltonian 속 specific term과 직접적으로 연관되지 않는 model Hamiltonian이기 때문이다.
최근, first principal methods를 이용해서 interfaces에서의 Rashba coefficient를 계싼하려는 여러 시도가 있었다. 이 연구에서의 가장 중심적인 schemeㅇ은 _____
24.3. Current-driven spin torque with Rashba coupling
기존의 전류 구동 스핀 토크의 경우, spin valve와 같이 noncollinear magnetization 상태가 필요하다. 이 시스템들에서는, 스핀 토크가 스핀분극전류로부터 전달되는 각운동량의 변화로부터 발생한다. Rashba Hamiltonian은 이와는 다르게 작용한다: Rashba system에서는 전도전자에 운동량-의존-자기장이 발생하며 시스템 속에서 전류가 흐르는 상태일 때, 전자의 운도량 합이 0이 아닌 이상 알짜 자기장이 발생한다. 전류에 의해 발생하는 유효 자기장을 조금 더 자세히 계산하기 위해서 아래와 같이 강자성체 금속에서의 전도전자에 대한 단순화 된 모델을 고려해보자.
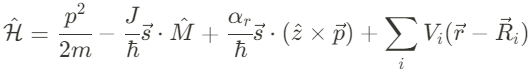
For a magnet, this same splitting is modified
by the exchange field resulting in a large magnetic anisotropy energy via the Dzyaloshinskii-Moriya
mechanism. This different, yet traditional, path to an electrically induced anisotropy energy can explain the
electric field, thickness, and material dependence reported in many experiments.
There is a Rashba splitting of the band structure
leading to a quadratic, $(E_{int}+E_{ext})^2$, contribution to the magnetic anisotropy, contrasting with a linear in $E_{ext}$ doping effect.
'Magnetotransport' 카테고리의 다른 글
| Physics Origin of Universal Unusual Magnetoresistance (0) | 2025.07.15 |
|---|---|
| Magnetotransport Part 2. Hall Effects (1) | 2023.12.06 |
| Magnetotransport Part1. Magnetoresistance (1) | 2023.12.05 |


댓글