참조 문헌
[1] Magneto transport. Family of Hall effects and AMR effects, Vadim Zayets
[2] Fundamentals of Magnetism, Getzlaff (2010)
[3] Magnetic Memory Technology, Denny D. Tang, Chi-Feng Pai (2020)
0. Introduction
Magnetotransport는 자기장(강자성체에서는 자화가 그 역할을 할 수 있다)내에 물체가 놓여있을때 물체 내 전자의 수송 현상을 포괄하는 명칭이다. 이 magnetotransport와 관련된 측정은 크게 두가지로 나뉘어진다. 일반적으로 아래와 같은 Hall bar가 있을 때, 전류 $I_\mathrm{C}$ (= $I_\mathrm{xx}$) 방향과 평행한 방향으로 전압($V_\mathrm{xx}$)을 측정하는 것을 magnetoresistance, 그리고 이와 수직한 방향으로 전압($V_\mathrm{xy}$)을 측정하는 것을 Hall effect라 한다.
대표적인 magentoresistance와 Hall effect는 아래와 같이 나타낼 수 있다
| Magnetoresistance | Hall Effect |
| Ordinary Magnetoresistance | Ordinary Hall Effect |
| Anisotropic Magnetoresistance | Anomalous Hall Effect |
| Spin Hall Magnetoresistance | Spin Hall Effect ($\leftrightarrow$ Inverse Spin Hall Effect) |
| Unidirectional Spin Hall Magnetoresistance | Quantum Hall Effect |
| Giant Magnetoresistance | Integer Quantum Hall Effect |
| Tunneling Magnetoresistance |
해당 글에서는 위에 제시된 대표적인 MR과 Hall effect를 하나씩 살펴보고자 한다.
1. Magnetoresistance (MR)
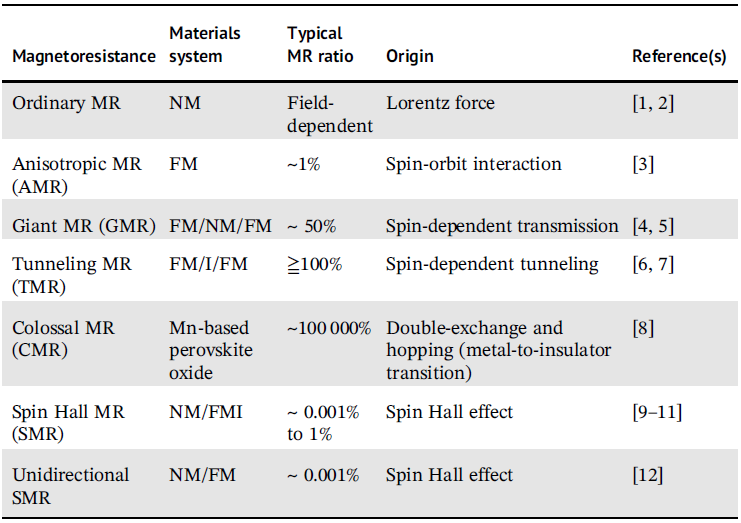
Magnetoresistance는 위에서 언급했듯이, 채널 전류와 평행한 방향으로의 전압을 측정할때, 자기장(또는 스핀)의 방향에 따라 저항이 바뀌는 현상이다. Magnetoresistance의 경향이나 이에 대응하는 MR ratio(작용하는 자기장에 맞춰 변화하는 MR value의 퍼센티지)는 서로 다른 물질 시스템에서 매우 다르게 나타난다. 예를 들어, 아래 표에 나와있듯이, 강자성체 물질 내에서 가장 먼저 발견된 anisotropic MR (AMR)의 경우 일반적으로 1%정도의 MR ratio를 갖는다. 하지만, 적절한 박막 증착 엔지니어링을 통해 , TMR은 MR ratio가 100%보다 클 수도 있다.
큰 MR ratio를 갖는 물질 시스템이나 박막 스택 구조를 찾는 것은 실행 가능한 MRAM을 개발하는 주요단계이다, 왜냐하면 큰 MR 효과는 memory readout을 증가시키기 때문이다. 예를 들어, 최신의 산업-레벨의 STT MRAM의 경우, TMR ratio는 높을 경우 200%까지 도달 할 수 있다.
| Magnetoresistance | Materials System | Typical MR ratio | Origin |
| Ordinary MR | NM | Field-dependent | Lorentz force |
| Anisotropic MR (AMR) | FM | ~ 1% | Spin-orbit interaction |
| Spin Hall MR | NM/FMI | ~ 0.001% to 1% | Spin Hall effect |
| Unidirectional SMR | NM/FM | ~ 0.001% | Spin Hall effect |
| Giant MR (GMR) | FM/NM/FM | ~ 50% | Spin-dependent transmission |
| Tunneling MR (TMR) | FM/I/FM | $ \ge $ 100% | spin-depndent tunneling |
1.1. Ordinary Magnetoresistance (OMR)
일반적으로, 소자에 자기장이 걸리면 저항이 증가하는 현상이 발생한다. 이는 ordinary Hall effect와 똑같은 원리로 자기장이 Lorentz force를 작용시켜 전자의 궤적을 휘게하여, effective mean free path가 감소하여 발생하는 현상이며, 일반적으로 자기장의 제곱에 비례하는 경향을 보인다.

하지만 몇몇 강자성체 물질에서는, OMR보다 더 낮은 속도로 저항이 증가하는 현상이 나타나는데, 이는 전자 scattering과 연관된다. 아래 그림과 같이 강자성체는 큐리온도 아래에서는 band splitting이 일어나 강자성의 특성을 보이며, 큐리온도보다 높은 곳에서는 band splitting이 상쇄되어 상자성의 특징을 보인다. 상자성 상태에서는 Fermi energy 부근에 d-orbital이 많이 분포하고, 이로인해 s-orbital의 전도전자가 d-orbital로의 transition(scattering)이 많이 일어나 저항이 증가한다. 반면에 강자성 상태에서는 band splitting으로 인해 Fermi energy 부근에 d-orbital이 위치하지 않고, 이로 인해 s-orbital속 전도전작가 d-orbital로의 scattering이 일어나지 않음에 따라 저항이 증가하지 않는 것이다. 이 현상은 추후에 확인할 GMR과 매우 유사하기에 숙지하면 좋다.

1.2. Anisotropic Magnetoresistance (AMR)
Anisotropic Magnetoresitance는 전류(I_xx)와 자기장(자화) 사이의 상대적인 방향에 따라 저항이 바뀌는 현상으로, longhitudinal voltage(V_xx)를 통해 측정된다. AMR은 William Thomson에 의해 처음 발견되었고 Lord Kelvin에 의해 알려졌으며, 모든 자성 물질에서 이 현상이 나타나는 것으로 알려져있다. AMR의 근원은 spin-orbit interaction이며, 이 상호작용은 전도 전자(itineant electrons)의 전도 특과 물질의 자화 (localized electrons)를 이어준다. 일반적으로, resistivity $\rho$는 $\pi$에 다음과 같은 관계식을 갖는다.
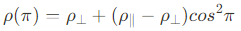
여기서 $\rho_{\perp}$과 $\rho_{\parallel}$는 각각 전류가 자화와 수직일때와 수평일때의 물질의 resistivity이다. 일반적인 강자성체의 AMR ratio는 는 아래와 같이 표현 될 수 있으며 수%이하의 값을 갖는다.


Spin-orbit interaction이 존재하는 system에서는 spin-flip scattering이 허용 된다. 다시 말해 majority spin의 s-orbital 속 전자가 minority spin의 down-spin 을 향하는 d-orbital로 scattering(transition) 할 수 있다는 것이다. 이는 scattering의 증가를 야기하고 결국 저항 값의 증가를 나타낸다. 또한 orbital의 각도에 따른 Fermi energy 부근에서의 d-orbital의 DOS 변화에 따라 각도 별로 저항 값이 바뀐다.

1.2. Spin Hall Magnetoresistance (SMR)
SMR은 spin Hall effect에 의해 물질의 longitudinal resistance가 변화하는 현상이다. 전기장에 의해 물질 내에서 한쪽 방향으로 흐르는 전자는 spin Hall effect에 의해 $I_\mathrm{xx}$와 $\vec{\sigma}$에 동시에 orthogonal한 방향으로 휘게된다. 이는 결과적으로 도체 내 모서리 부근에 전자의 축적을 야기하게 되는데, 이때 NM에 인접한 FM이 있을 경우 모서리에 축적된 전자는 FM의 자화와 상호작용하여 spin-transfer torque를 겪게 된다. 만약 전도 전자의 스핀이 FM의 자화와 평행하다면, 전자는 스핀의 방향이 변하지 않은채로 모서리에서 튕겨져 나오게 되지만, 만약 전도 전자의 스핀이 FM의 자화와 수직하다면, spin의 방향이 torque로 인해 반대방향, 또는 기존의 $I_\mathrm{xx}$방향에서 휘어진 방향으로 왜곡된 채 튕겨져 나올 수 있다. 결과적으로 이 튕겨져 나온 전자의 스핀 방향에 따라 inverse spin Hall effect가 발생했을 때 기존의 $I_\mathrm{xx}$의 component로 다시 참여할지, 아니면 I_\mathrm{x\gamma} 방향의 전류를 만들어 기존의$I_\mathrm{xx}값을 줄이게 될지 결정하게 된다.
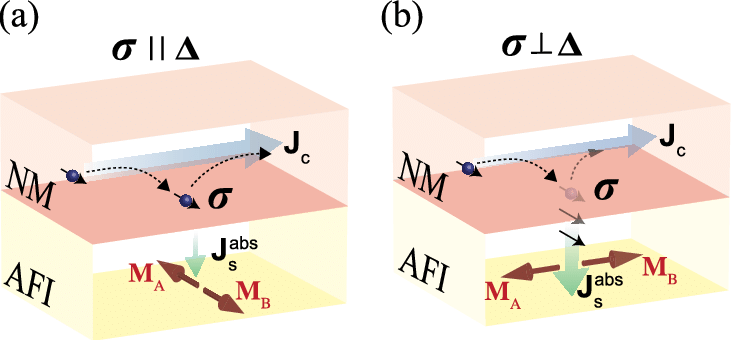
이는 결과적으로 전류의 방향과 FM의 방향이 평행 할 때 channel 내 캐리어의 수를 줄여(I_xx 감소) 저항을 높이는 효과를 만들어내고, 전류의 방향과 FM의 방향이 수직할 때 channel 내 캐리어의 수를 높여(I_xx 증가) 저항을 줄이는 효과를 만들어낸다.
1.4. Unidirectional Spin Hall Magnetoresistance (USMR)
우선, 이 점 하나를 명확하게 하고자 한다. SMR과 USMR은 모두 같은 시스템에서 발생하는 효과로, 다만 차이점은 SMR은 1st harmonic, USMR은 2nd harmonic이라는 점이다.
Unidirectional magnetoresistance (UMR)은 강자성체의 계면과 bulk에서 나타나는 스핀 홀 효과, 혹은 라쉬바-에델스타인 효과에 의한 스핀 주입과 축적, spin-dependent scattering, magnon scattering과 연관된다. 하지만, 입자가 움직이는 방향은 시간의 반전에 대하여 symmetric 하다고 언급하는 Micrscopy irreversibility의 법칙으로 인해, 대부분의 magnetoresistance 현상들은 전자가 흐르는 방향에 의존성을 띄지 않는다.(예를 들어, 전류의 방향과) 최근들어 우리는 이 현상에 대한 예외를 찾아냈다, 이를 unidirectional(한쪽방향을 선호하는) magnetoresistance라 명명하고, FM/NM bilayer 시스템에서 전류를 인가할 때, 전류의 부호에 따라 MR에 차이가 있는 현상이다. 이 기이한 MR은 SMR과 마찬가지로 spin Hall effect를 기반으로 하고 있다. Ta, Pt와 같은 HM에서는 conductor의 각 모서리, 계면에 같은 방향의 스핀을 가지는 전자들이 축적된다. 만약 그 계면에 junction으로서 FM에 위치하게 되면, 전체 전기저항은 SHE에 의해 축적된 한쪽 방향 스핀 전자들과 강자성체 자화의 상대적인 alignment에 의해 결정된다.
참고문헌
Unidirectional Spin Hall Magnetoresistance in Antiferromagnetic Heterostructures doi.org/10.1103/PhysRevLett.130.086703
Harmonic measurement in ��/��2�3
When an AC current �=�0���(��) is applied, due to spin-orbit torque and thermoelectric effect, the measured voltage becomes

�1� and �2� are called first and second harmonic voltage that can be separately measured using lock-in amplifier. The first harmonic voltage is the same as DC measurement
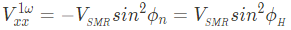

Here �� is the in-plane angle between applied field and current direction, and ��=��+�2 is the direction of Neel vector.
For the second harmonic voltage, it contains three parts
- Spin Seebeck effect (SSE)
- field-like torque
- USMR
For SSE, the proportional relation belows satisfies.

Thus

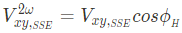
For field-like torque,

Then


where the equation below is the field-like torque induced Neel vector rotation from its equilibrium position.

The rest is the USMR,
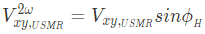
Then second harmonic voltage can be rewritten as


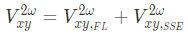
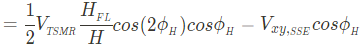
Notice that USMR only shows up in the ���2� term. To extract the USMR contributions, we first fit the ���2� and ���2� to get the ���,���+���,���� and ���,���; Then, V_{xx,USMR} can be separated given that

Compared wi the fitting to ferromagnets, the transverse second harmonic voltage does not contain damping-like (DL) torque term, which makes the fitting more reliable.
the change of the resistance of a material on rotation of the magnetization
the SHE causes an unusual magnetoresistance associated with the back-flow of a spin current into the NM when the spin accumulation

is aligned with the magnetization of the FM, which increases the conductivity of the NM due to the inverse SHE (refs 17, 18, 19, 20). This so-called spin Hall magnetoresistance
USMR
Linear response 영역에서의 방향 의존성은 spin Hall magnetoresistance(SMR)이라 한다. 다른 SHE 연관 MR은 non-linear 영역에서도 나타나는데, $\vec{\sigma}$이 $\vec{M}$과 동일선상에 있을 때, $\vec{\sigma}$이 $\vec{M}$과 평행 할 때의 저항과 반평행 할 때의 저상은 서로 다르다.
$\vec{\sigma}$는 전류밀도의 방향에 따라 부호가 달라지기에, current 방향에 따른 asymmetry를 보인다고 할 수 있다. 이러한 nonlinear 영역에서의 의존성은 unidirectional spin Hall magnetoresistance라 한다. 그러므로, USMR의 크기는 J와, $\vec{\sigma}$ 그리고 $\vec{M}$ 사이의 상대적 방향에 따라 결정된다. 다시 말해, spin configuration에 따라 시스템 속 longitudinal resistance에 asymmetry가 결과로 나타나는 것이다.
일반적으로 두개의 서로 다른 USMR 메커니즘이 제시된다. 하나는 FM layer에서의 electron-magnon scattering의 전류-방향-의존성이며, 다른 하나는 FM/NM 계면에서의 스핀 축적에 대한 전류-방향-의존성이다.
이 장에서 살펴보는 다른 MR과는 반대로, USMR은 chirality를 수반한다.
우리가 강자성 부도체를 NM위에 위치시킬 때, 다음과 같은 일들이 벌어진다.
비록 전자들이 metal

When we put a ferromagnetic insulator on top of this nonmagnetic metal, the following happens. Although the electrons can not flow out of the metal and into the magnetic insulator, the electron spin current can be converted into a magnon spin current at the interface of the bilayer.
Microscopically, an electron spin that reaches the interface will flip its orientation creating a magnon(by conservation of angular momentum) in the ferromagnet.
Let's limit our attention to only the nonmagnetic metal, this dissipation of electron spin current into the magnet can be interpreted as a small effective spin current in the metal.
Effective spin current는 initial charge current에 의해 만들어지는 electron spin current와 같은 방향을 향할 것이다. 예를 들자면, spin down electron들이 계면 근처에 축적됐다고 하자. 이때 magnon을 생성함으로써, 이 전자의 스핀은 뒤바뀌게 되어 spin up electron이 될것이다. 이렇게 생성된 spin up electron은 마치 FM에서 주입되는 것 처럼 NM 계면에서 NM bulk로 diffusion된다. down이 위를 향하다가 up이 아래를 향해 가므로 spin current의 방향은 동일한 것이다. 하지만 effective spin current가 ISHE를 통해 발생시키는 charge current는 본래 NM의 전류와는 반대방향으로 향하게 된다. (잘 보면 안다). The resulting resistance is known as the unidirectional spin Hall magnetoresistance (USMR).
The nonlinear dependence of the USMR on the direction of the electric field appears as a result of the spin Hall effect.
Depending on the direction of the electric field, either spin down or spin up electrons accumulate near the interface. Since the magnetization direction of the ferromagnetic layer is fixed, these spins are either parallel or antiparallel to this magnetization. It turns out from the experiments performed by Avci et al. that a parallel alignment leads to a high resistance whereas an antiparallel alignment leads to a low resistance.
Having explained the USMR and its nonlinear character, we now set out to find the magnon contribution. We first summarize results. Putting all the different currents together and considering only the accumulation dependent part of the interfacial spin current, we have
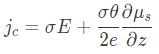
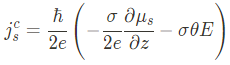
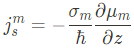

For our purpose we need to know the charge current.
Therefore, the equations above must first be solved for the accumulations �� and ��.
Following the diffusion equations, these accumulations generally look like
1.5. Giant Magnetoresistance (GMR)
Giant Magnetoresistance (GMR)은 서로 교차하는 전도성 강자성체, 비자성체 적층구조에서 발견되는 양자역학적 MR이다. 이 GMR은 Albert Fert와 Peter Grunberg에 의해 독립적으로 발견되었으며 이 두 과학자는 GMR을 발견한 공로로 2007년 노벨물리학상을 수상한다.

GMR은 인접한 강자성체 사이의 정렬이 평행하냐, 반평행하냐에 따라서 전기적 저항이 바뀌는 효과로, 강자성체가 평행할 때는 저항이 낮으며 반평행 할때는 저항이 높다. 강자성체 금속/비자성 금속/강자성체 금속 (FM/NM/FM) 샌드위치 구조는 외부 자기장을 통해 평행/반평행 조절이 가능하다. 이 trilayer를 가로지르는 전기저항의 크기는 두 FM layer의 자화의 상대적인 configuration에 따라 달라진다. 두 FM layer의 자화 방향이 서로 평행(P)할 때의 저항은 반평행(AP)할 때 보다 더 작은데, 이는 아래의 그림을 통해 쉽게 이해할 수 있다.

일반적으로 두 강자성체 평행한 경우에 FM1/NM/FM2의 스핀 밸브 구조에서는 아래와 같은 메커니즘으로 전자의 흐름이 결정된다.
- FM1 속 majority spin은 Fermi energy 부근에 d-orbital이 부재하여 많은 전자들이 FM2로 흐르게 된다.
- 마찬가지로 FM2에서도 Fermi energy 부근에서 majority spin의 d-orbital DOS가 없기에, conductivity는 유지되며 많은 majority spin이 FM1/NM/FM2 스핀 밸브 채널을 통과한다
- FM1 속 minority spin은 Fermi energ 부근에 d-orbital의 DOS가 많기에 많은 scattering이 발생하며, 이로 인해 높은 저항으로 적은 전류가 흐른다.
- 적은 전류만이 FM2로 흐른 minority spin은, 여기서도 Fermi energy 부근 d-orbital의 큰 DOS로 인해 또 다시 scattering이 발생하며 거의 전류가 흐르지 않는다.
결과적으로 FM1/NM/FM2 스핀 밸브 구조에서 두 자화가 서로 평행하면 majotiy spin의 전류가 주가 되어 낮은 저항대를 형성한다.
- FM1 속 majority spin은 Fermi energy 부근에 d-orbital이 부재하여 많은 전자들이 FM2로 흐르게 된다.
- 하지만 이번에 FM2에서는 (FM1의) majority spin의 d-orbital이 큰 DOS를 가져 많은 전자가 scattering 되어 d-orbital로 종속된다.
- FM1 속 minority spin은 Fermi energ 부근에 d-orbital의 DOS가 많기에 많은 scattering이 발생하며, 이로 인해 높은 저항으로 적은 전류가 흐른다.
- 적은 전류만이 FM2로 흐른 (FM1의) minority spin은, 이번에는 Fermi energy 부근 d-orbital의 DOS가 존재하지 않아 해당 전류를 유지한채 그대로 흐를 수 있다.
결과적으로 FM1/NM/FM2 스핀 밸브 구조에서 두 자화가 서로 반평행하면, 주가 되는 spin이 없기에 낮은 전류를 형성하여 높은 저항대가 만들어진다.
AMR 특정 FM/NM/FM heterostructure에서의 GMR의 크기는 GMR ratio에 따라 특정 될 수 있다. GMR ratio는 아래와 같이 쓸 수 있다.
$ \cfrac{R_{AP}-R_{P}}{R_{AP}} $
여기서 $R_{AP}$과 $R_{P}$는 각각 AP상태일때의 저항과 P상태일때의 저항이다.
위에서 설명한 내용을 수식적을 나타내보고자 한다. spin-up(down) 전자들이 자화의 방향이 up(down) 상태인 FM layer를 통과할때, 채널의 저항은 $R_{\uparrow \uparrow}$ ($R_{\downarrow \downarrow}$)이다. 반대로, spin-up (down) 전자들이 자화의 방향이 down(up) 상태인 FM layer를 통과할 때는 채널의 저항이 $R_{\uparrow \downarrow}$ ($R_{\downarrow \uparrow}$)이다.
일반적으로 $R_{\uparrow \downarrow}>R_{\uparrow \uparrow}$ 이다. 약간의 수학을 얹으면 GMR ratio를 얻을 수 있다.

이후에, GMR은 그자체로서 자기장을 센싱하는데 효과적인 방법임이 증명됐고, HDD read head와 초기 MRAM 기술에 혁명적인 발전을 이끌었다.
1.6. Tunneling Mangetoresistance (TMR)
FM/NM/FM 샌드위치 구조(spin-valves)와 유사하게, FM/insulator/FM MJ는 또한 MR 효과를 가질 수 있다. 이는 두개의 FM 전극 사이에서 적절한 insulator가 tunnel barrier로서 존재할 때 양자역학적 터널링을 통해서 발현된다. 이로 인해 나타나는 효과는 TMR이라 불리며, 적절한 물질의 조합과 film stack 엔지니어링을 곁들인다면 일반적으로 GMR보다 오더 이상의 차이가 발생한다.

14%정도의 TMR이 처음 실험적으로 Julliere에 의해 1975년에 극저온의 Fe/(Oxidized-)Ge/Co 시스템에서 발견되었으며, 이는 GMR의 발견보다도 빠른 것이었다. Jullier's 이론은 TMR ratio가 다음과 같이 표현 될수 있음을 보여준다.
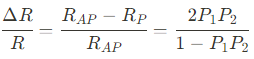
여기서 $P_{1}$과 $P_{2}$는 각각 두 강자성체 전극의 스핀 분극 값을 나타낸다. 스핀 분극 P는 spin-up과 spin-down 전자의 Fermi level에서의 density of states $N_{S}$와 연관되며 다음과 같이 나타낼 수 있다.
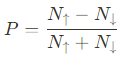
Julliere의 공식에 따르면, 두개의 P1, P2는 1에 가까울 수 있으며, 이 경우 TMR ratio는 1보다 상당히 커지게 된다. 하지만, tunnel barrier와 FM 전극의 전자구조 사이의 상호작용이 위의 식에서는 빠져있다. 이후의 실험과 증명된 이론들에 따르면 barrier의 종류 뿐만 아니라 interface의 품질역시 높은 TMR을 얻는데 주요 요소로 자리잡고 있음을 보여준다.
상온에서의 giant TMR은 Moodera 연구진과 Miyazaki 연구진에 의해 $Al_{2}O_{3}$ 배리어를 사용한 MTJ에서 독립적으로 처음 발견되었으며 이는 Julliere의 연구 이후 20년 만의 일이다. $CoFe$/$Al_{2}O_{3}$/$Co$ 에서는 11.8%의 TMR이, $Fe$/$Al_{2}O_{3}$/$Fe$ 에서는 18%의 TMR이 발견되었다.

2004년에, 또 다른 패러다임의 변화가 발견되었는데, 이는 상온에서 200%에 가까운 TMR이 MgO-기반의 MTJ에서 발견되었기 때문이다. 이는 sputtering technique를 이용한 Parkin 연구진과 epitaxial growth를 이용한 Yuasa 연구진에 의해 발견되었다.(Figure 4.6을 확인한다). 비록 2001년에 여러 이론적인 연구들이 MgO-기반의 MTJ에서 높은 TMR을 예측했지만, 높은 TMR을 구현하는 것은 Fe(001)/MgO(001)의 lattic match를 물질 성장에 있어서 잘 컨트롤 함을 요구한다.
Amorphous CoFeB를 FM layer로 사용하고 post-fabrication annealing을 수행하는 것은 상온에서의 TMR을 200% 이상으로 향상시킨다. 현재로서는, 스퍼터링을 통해 증착되고 적절한 annealing 과정을 거친 CoFeB/MgO/CoFeB trilayer가 연구와 잠정적인 산업 레벨의 MRAM응용에 가장 많이 사용되는 MTJ 구조이며, 약 600% 정도의 TMR을 가진다.
4.1. Introduction
챕터3에서, 우리는 magnetic material의 물리적 성질에 대해 다뤘다. 특히 epitaxial growth, 혹은 sputtering으로 증착된 박막형태에 대해서 다뤘다. 이 material system에 전류를 흘려줬을 때 풍부한 물리적 성질을 우리는 발견할 수 있다. 이, 소위 transport properties라 불리는, 물리적 성질들은 자기장 혹은 자화가 존재할 때 물질의 전기적 저항과 연관되어 있으며 각각 서로 다른 종류의 magnetoresistance(MR)로 카테고리화 된다. MR의 행동 변화와 이에 따른 MR ratio(작용한 자기장에 따른 MR의 변화 정도)는 서로 다른 material system마다 매우 다를 수 있다. 예를 들어, Table 4.1.에 나온것 처럼, 가장 초기에 발견된 강자성체 시스템에서의 anisotropic MR (AMR)의 일반적인 MR ratio는 1% 남짓이었다. 하지만, 적절한 film stack engienering을 통해, MR ratio는 100% 이상으로도 커질 수 있으며 TMR의 경우 특히 그렇다.
큰 MR ratio를 갖는 Materials system, 혹은 thin film layer stack structure를 발견하는 것은 실제 작동 가능한 MRAM을 만드는 주요 열쇠이기도 하다. 왜냐하면 큰 MR 효과는 memory readout을 향상 시킬 수 있기 때문이다. 예를 들어, 최신의 industrial-level STT-MRAM의 경우 TMR ratio는 높을 경우 200%까지도 도달 할 수 있다.
이 챕터에서, 우리는 세 종류의 FM, 혹은 FM heterostructure에서 발견할 수 있는 MR effects에 대한 기본 정의들을 자세히 살필 것이다. 여기에는 AMR, GMR(giant magnetoresistance), TMR이 포함된다. 이 세 종류의 MR 효과들은 MRAM 뿐만 아니라 관련된 스핀트로닉스 응용분야에 가장 연관이 깊으며 기초가 된다.
4.2. Anisotropic Magnetoresistance
강자성체 물질에서, longitudianl resistance, 혹은 resistivity $\rho$는 흐르는 전류의 방향과 물질 자화 방향 사이의 각도 $\phi$ 에 따라 달라진다. 이를 AMR효과라 하며, Willim Thomson에 의해 가장 먼저 발견되었고 Lord Kelvin에 의해 알려지게 됐다. AMR의 근원은 spin-orbit interaction으로, 물질 내 전도전자(itinerant electrons)의 transport properties와 magnetization(localized electron) 사이를 연결해준다. 일반적으로, resistivity $\rho$는 $\phi$값에 의해 결정되며 아래와 같이 쓸 수 있다.
$\rho(\phi) = \rho_{\perp} + \left( \rho_{\parallel} + \rho_{\perp} \right) cos^{2}\phi $
여기서 $ \rho_{\perp} $와 $ \rho_{\parallel}$은 각각 자화가 물질에 흐르는 전류와 수직일때, 수평일때의 resistivity를 나타낸다.
일반적인 강자성체 물질의 AMR ratio는 아래와 같이 나타낼 수 있으며, 수 퍼센트 이내의 값을 갖는다.
$\cfrac{\Delta R}{R} = \cfrac{R_{\parallel}-R_{\perp}}{R_{\parallel}}= \cfrac{\rho_{\parallel}-\rho_{\perp}}{\rho_{\parallel}}$

Figure 4.1.은 AMR의 예를 나타낸다. 외부 자기장에 따른 저항 혹은 resistivity의 변화에 의해, AMR은 HDD read head와 field sensor로서 사용되기도 한다.
4.3. Giant Magnetoresistance (GMR)
강자성체 금속/비자성체 금속/강자성체 금속 (FM/NM/FM) 샌드위치 구조 이면서, 두 FM layer에서 각자 자화를 가지는 구조의 경우, 이 구조는 외부 자기장에 의해 컨트롤 될 수 있다. 이 trilayer를 통과할 때의 전기적 저항은 두 FM layer의 자화 방향에 따른 변수로 나타낼 수 있다. 두 FM layer의 자화 방향이 서로 평행 할 때(parallel, or P configuration), 저항은 낮으며 반대로 두 FM layer의 자화 방향이 서로 반평행 할때(antiparallel, or AP configuration) 저항은 높아진다. 이는 가장 유명한 GMR 효과의 가장 단순한 phenomenological picture이다. 특정 FM/NM/FM heterostructure의 GMR크기는 아래의 GMR ratio를 통해 나타낼 수 있다.
GMR ratio $= \cfrac{R_{AP}-R_{P}}{R_{AP}}$
GMR 효과를 현학적으로 설명하는 방법으로는, 전자가 맞닥뜨리는 첫번째 FM layer를 spin polarizer로 취급하는 것이다. 다시 말해 전도 전자가 첫번째 FM layer를 통과함으로써 부분적으로 spin-polarized 된다는 것이다. Spin-polarized electrons는 NM을 별다른 scattering 없이 통과하게 된다. 이후 두번째 FM layer에 도달 했을때, 전자가 layer의 magnetization과 같은 방향으로 정렬 됐을 때 확률적으로 더 잘 통과하게 된다. 반대로, 전자의 스핀 방향이 local moment의 반대방향으로 정렬되어 있는 경우, 더 많은 스캐터링을 마주하게 될 것이다. 이는 Figure 4.2에 묘사되어 있다.

Spin-up과 spin-down 전자를 두개의 평행한 회로(Fig4.2.)에 전하 캐리어로 간주하는 two-channel model은 GMR을 이해하는데 있어 준-정량적인 관점을 제공한다. Spin-up(down) 전자가 up(down) state의 자화를 가지는 FM layer를 통과할때, 채널의 저항은 $R_{\uparrow \uparrow}(=R_{\downarrow \downarrow})$이다. 다른 한편으로, spin-up(down) 전자가 down(up) state의 자화를 가지는 FM layer를 통과할때, 채널의 저항은 $R_{\uparrow \downarrow}(=R_{\downarrow \uparrow})$이다. 일반적으로, $R_{\uparrow \downarrow}>R_{\uparrow \uparrow}$이다. 약간의 수학을 곁들이면, GMR ratio는 아래와 같이 나타낼 수 있다.
$\cfrac{\Delta R}{R} = \cfrac{R_{AP}-R_{P}}{R_{AP}}= \cfrac{(R_{\uparrow \downarrow}-R_{\uparrow \uparrow})^2}{(R_{\uparrow \downarrow}+R_{\uparrow \uparrow})^2}$
Diffusive regime (Boltzmann equation 접근법)에서의 전도 전자의 transport와 관련된 Multilayer system에서의 GMR에 대한 더 상세한 이론은 Valet과 Fert에 의해 제안되었다.

GMR의 실험적 결과는 Binasch 연구팀에 의해 Fe/Cr/Fe 시스템에서, 그리고 Baibich 연구팀에 의해 Fe/Cr superlattice 구조에서 처음 빌견되었으며, Figure4.3에 나와있다. 측정되는 material system에 따라서, 그리고 measurement configuration (CIP 혹은 CPP)에 의해서 GMR ratio는 수 퍼센트에서 수십 퍼센트까지 변화할 수 있다. CPP configuration을 활용한 FM/NM/FM 구조는 spin-valves로 알려져 있으며, 이는 device의 two-terminal resistance가 외부 자기장에 따라 높은 저항(AP configuration)과 낮은 저항(P configuration) 사이를 왔다갔다 하기 때문이다. 이후에, GMR은 magnetic field를 sensing하는 매우 효과적인 수단으로서 자리 잡았으며, HDD read head와 초기의 MRAM 기술의 혁신을 이끌었다.
4.4. Tunneling Magnetoresistance (TMR)
FM/NM/FM sandwich structure (spin-valves)의 구조와 유사하게, FM/부도체/FM로 이루어진 MTJ또한 적절한 부도체를 tunnel barrier로 사용함으로써 두 FM electrodes 사이의 양자역학적 터널링을 통해 MR effect를 가질 수 있다. 이로 인한 결과로 나타나는 효과를 TMR이라 하며, 일반적으로 물질 조합과 film stack engineering을 통해 GMR보다 더 큰 TMR ratio를 가진다. 실험적으로 14% 정도의 TMR을 가지는 것이 Julliere에 의해 1975년 극저온의 Fe/(Oxidized-)Ge/Co system에서 발견되었으며 이는 GMR의 발견보다도 더 이른 것이었다. Julliere의 이론은 TMR ratio가 다음과 같이 표현될수 있음을 제안한다.
$\cfrac{\Delta R}{R} = \cfrac{R_{AP}-R_{P}}{R_{AP}}= \cfrac{2P_{1}P_{2}}{1-P_{1}P_{2}}$
여기서 $P_{1}$과 $P_{2}$는 두 ferromagnetic electrodes의 spin polarization 값을 나타낸다. Spin polarization P는 Fermi level에서의 spin-up 전자와 spin-down 전자의 density of states $N_{S}$와 관련되며 아래와 같이 나타낼 수 있다.
$P = \cfrac{N_{\uparrow}-N_{\downarrow}}{N_{\uparrow}+N_{\downarrow}}$
Julliere의 이론에 따르면, $P_{1}$과 $P_{2}$가 1의 값에 가까울 경우, TMR ratio는 1보다 더 큰 값을 가지게 된다. 하지만, 터널 배리어 역할의 중요성과 FM electrodes의 band structure 사이의 상호작용이 위의 단순한 식에서는 무시되어 있다. 이후의 실험과 개선된 이론은 배리어의 종류 뿐만 아니라 interface의 quality 여기 높은 TMR을 얻기위해 고려해야 된다는 것을 보였다.
상온에서의 high TMR은 Moodera 연구팀과 Miyazaki 연구팀에 의해 독립적으로 1995년 $Al_{2}O_{3}$ 터널 배리어를 가지는 MTJ에서 처음 발견 되었다. 이는 Julliere의 연구 이후 20년 만에 처음 발견이었다.
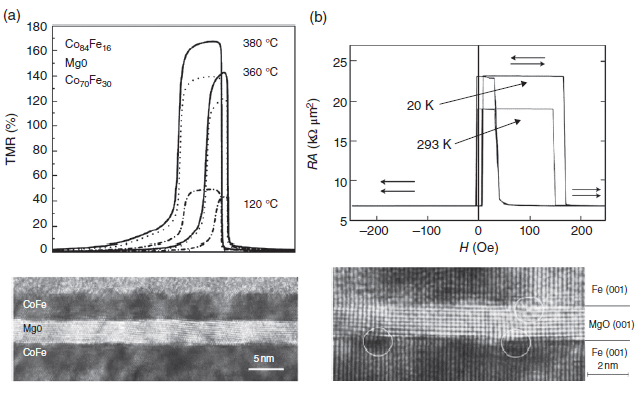
$CoFe/Al_{2}O_{3}/Co$에서는 11.8%의 TMR과 $Fe/Al_{2}O_{3}/Fe$junction에서는 18%의 TMR이 보고 되었으며, Figure4.5에 나와있다.

2004년에는, 또다른 패러다임 변화가 나타났는데, 바로 Parkin 연구팀에 의해 sputtering으로, 그리고 Yuasa 연구팀에 의해 epitaxial growth 기법으로 MgO 기반의 MTJ에서 상온 TMR이 거의 200%에 육박하는 결과가 나온 것이다.
Although several theoretical works that predicted high TMR in MgO-based MTJ were published in 2001, it turned out that the realization of high TMR in this system requires good control of Fe(001)/MgO(001) lattice match during material growth.
Using amorphous CoFeB as the FM layer and performing post-fabrication annealing can further enhance the room temperature TMR to greater than 200%.
Currently, sputtered CoFeB/MgO/CoFeB trilayer treated with the suitable annealing process is still the most common MTJ structure for both reasearch and tentative industrial-level MRAM applications, with the highest reported TMR ~600%
4.5. Contemporary MTJ Designs and Characterization
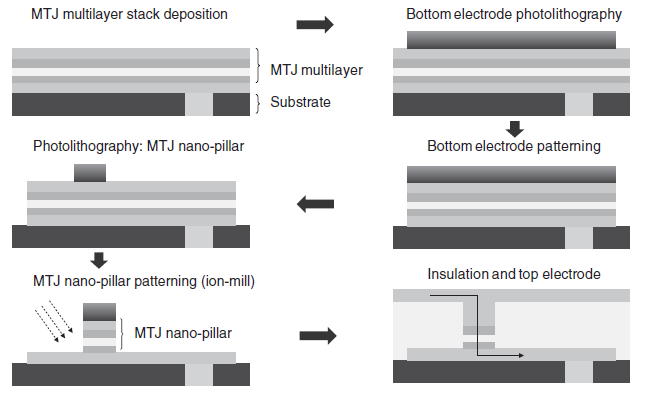
실제 메모리 응용면에서, MTJ(CPP configuration) 공정은 Figure 4.7.과 나와있다 싶이 전형적인 BEOL(back end of line) CMOS 기술을 기반으로 한다. 이는 일반적으로 sputtering system에 의한 MTJ layer stack deposition으로부터 시작하며, photolithography와 후속 etching steps등을 거쳐 nanopillar 모양의 MTJ devices를 정의한다. 하지만 추가적인 노력들이 산업적인 레벨의 표준을 맞추기 위해 MTJ를 공정하는데 있어 필요하다. 예를 들어, 높은 퀄리티의 MgO tunnel barrier를 포함한 다층박막을 증착하는 것과, ferromagnetic layer의 crystallization을 matching하는 것을 컨트롤 하는 것은 자성층의 높은 TMR ratio와 강한 PMA를 얻는데 매우 중요하다. 이 목표를 이루기 위해, 진보된 스퍼터가 개발되어야 한다. 리소그래피와 이어지는 ion milling(etching/patterning) 과정 역시 나노스케일에서 높은 수율과 높은 TMR의 MTJ를 획득하는데 매우 중요하다.
이 복잡한것들은 차차하고, 이 챕터의 마지막 부분에서, 우리는 가장 기초적인 MTJ layer stack design과 현대 MRAM application을 위한 characterization을 소개하고자 한다. The first one is the first demonstration of MgO-based
MTJ with FM layer being perpendicular magnetic tunnel junction (p-MTJ). The second one is a full p-MTJ structure with synthetic antiferromagnetic (SAF) layer, showing how complicated the MTJ layer design can be for modern MRAM. Finally we will briefly discuss a technique to characterize TMR from MTJ layer stack structures without patterning those films into micron-scale or nano-scale devices, which can facilitate the film optimization process.
4.5.1. Perpendicular MTJ (p-MTJ)
현대의 MTJ는 일반적으로 터널배리어로서 MgO를 이용한다. CoFeB 강자성체 합금 레이어는 일반적으로 FM 전극에 사용된다. Ta와 같은, 적절한 buffer layer를 이용하여 Ikeda 연구팀은 2010년 Ta/CoFeB/MgO heterostructure가 annealing 이후에 품질이 괜찮은 PMA를 얻을 수 있다는 것을 보였다. 이때 CoFeB 레이어의 두께는 1nm 정도로 매우 얇았다.
얇은 CoFeB 레이어를 이용한 Ta/CoFeB/MgO/CoFeB/Ta 레이어의 디자인은 그러므로 p-MTJ로 만들 수 있었으며, Figure 4.8과 같이 최대 40nm의 직경까지 줄일 수 있었다. Easy-axis를 정의하기 위해 shape anisotropy를 이용했던 기존의 in-plane MTJ와는 다르게, p-MTJ 디자인은 easy axis를 film의 수직방향으로 가질 수 있게끔 하여, 실제적인 MRAM 응용의 실현 가능성과 potential memory density를 증가시켰다. 또한 MgO 기반의 물질 시스템이 FM layer에 인접했을때 동시에 높은 TMR(~100%)과 PMA를 얻는다는 것은 놀라운 일이며 다양한 현대의 STT-MRAM 디자인의 가장 근본적인 레이어가 되게끔 만들었다.

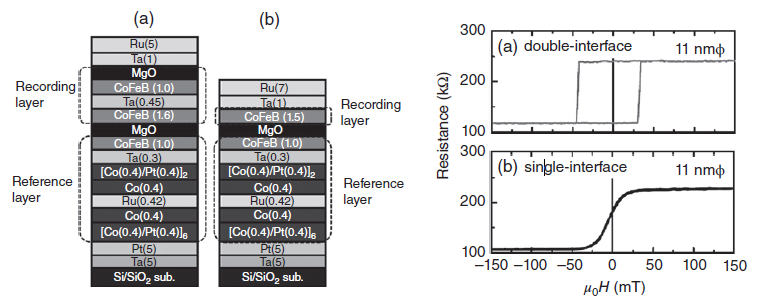
4.5.2. Fully Functional p-MTJ
Figure 4.8을 유심히 본다면, 이전 섹션에서 언급된 p-MTJ는 자기장이 없을 때 오직 한개의 안정적인 state (P state 혹은 low resistance state)를 가진다는 것을 알 수 있다. 이는 자기장이 없기 때문에 두개의 CoFeB layer의 자화가 강자성체 커플링을 가지는 경향을 가지고 그러므로 parallel state는 에너지적으로 선호되기 때문이다. 위에 언급된 p-MTJ를 완전히 작동하는 메모리 요소로 만들기 위해서는, 두 P와 AP state가 field가 없을때 안정적이게끔 만들기 위해 extra layer를 필요로 장착해야 된다. 이는 일반적으로 SAF layer를 이용한 CoFeB 레이어들 중에 effectively pinned된 한개의 레이어를 이용함으로써 얻을 수 있다. 이 경우, SAF 구조는 Figure4.9와 같이 $[Co/Pd]_{6}/Co/Ru/Co/[Co/Pd]_{2}$ 다층구조를 이용하여스며 여기서 발생하는 RKKY interaction을 활용했다. 추가적인 $Ta/CoFEB/MgO$ layer는 또한 recording layer의 PMA를 증가시키기 위해 구조에 포함되었다. 결과적인 MTJ는 높은 TMR을 얻을 수 있으며, zero field에서 bi-stable 저항 states를 가지고, 11nm 직경까지 스케일링이 가능하다.
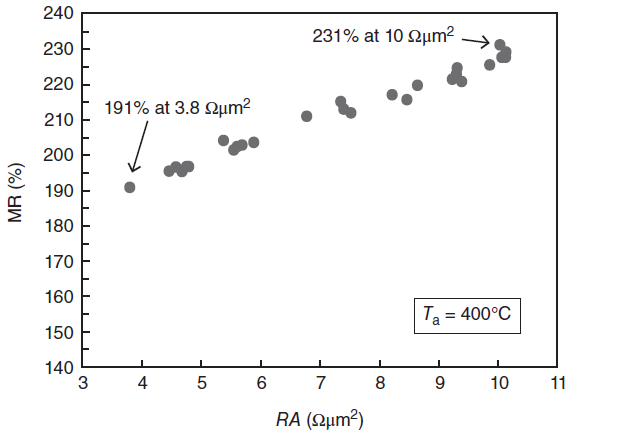
후의 챕터에서, 우리는 이 p-MTJ memory device의 writing mechanism을 소개할것이다. 이 메커니즘은 current-induced spin transfer torque 법칙을 기반으로 하며 이를 통해 CoFeB의 자화를 스위칭한다. CoFeB 자화를 바꾸는데 필요한 switching current를 줄이기 위해, resistance area (줄여서 RA라고 부르며, 터널 배리어의 두께와 근본적으로 상응한다.) 는 작으면 작을술고 좋다. 하지만 RA를 줄이는 것은 TMR의 퀄리티를 낮추낟. 최근의 연구적 노력들은 이 두 factor상의 trade-off limit을 한 차원 늘리는데 공을 들이고 있다. 예를 들어 Figure 4.10처럼 200%의 TMR ratio를 가지면서 5$\Ohm \mu m^{2}$의 RA를 가지는 경우를 말한다. 더 높은 TMR ratio와 상대적으로 낮은 RA를 가지는 것이 차세대 MRAM의 핵심 개발 열쇠라고 할 수 있을 것이다.
4.5.3. CIPT Approach for TMR Characterization
완벽하게 작동하는 MTJ 소자를 만들기 위해서, 길고 긴 공정 단계가 필요하다. 여기에는 다층 film stack을 증착하는 것과, 기둥 모양의 MTJ를 만들기 위한 리소그래피, 에칭 공정, bottom electrodes와 top electrodes를 분리시키기 위한 passivation 공정등이 포함된다. 이러한 과정은 각 공정 flow의 스텝들에 대해 적절한 레시피를 만들기 위해 잘 훈련된 엔지니어 팀 여러명이 달라붙어도 수개월 혹은 수년이 걸릴 수도 있다. 이 시간 오래걸리는 과정을 우회하고, 패터닝 되지 않은 증착 film의 TMR 특성을 characterization 하기 위해서, 새로운 probing 방법들이 개발될 필요가 있다. Current-in-plane Tunneling(CIPT) 방법은 패터닝 되지 않은 film 샘플에 프로브 세트만을 연결 함으로써 MTJ의 특성을 측정할 수 있는 효과적인 방법임이 밝혀졌다. CIPT 측저의 경우, 패터닝되지 않은 film의 sheet resistance가 기본적인 four-point-probe 방법을 이용해 측정된다. 전류는 두개의 전류 프로브에 의해 전달되고, 전압차가 또 다른 두개의 전압 프로브에 의해 감지될 것이다. 이를 통해 샘플의 저항을 계산할 수 있다.
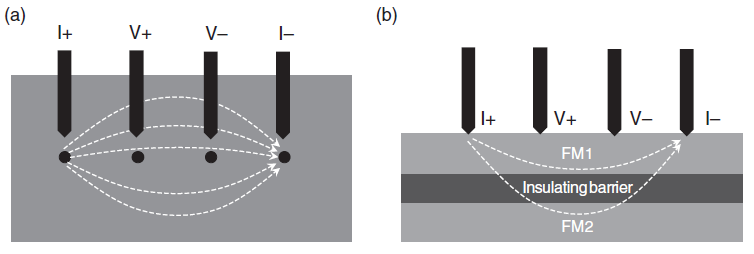
하지만, 전류가 한쪽 프로브에서 다른쪽 프로브로 흐를때, 전류와 전압 프로브 사이의 거리가 current distribution을 결정하는데 매우 중요하다. 만약 두 프로브가 너무 가깝다면, barrier를 터널링 하는 전류는 없을 것이며 TMR 효과도 보지 못할 것이다. 반대로, 만약 두 프로브가 너무 멀리 떨어져 있다면, 전류는 단순히 두개의 FM layer를 평행하게 흐를 것이며 tunneling part는 무시해도 되는 contribution이 될 것이다. CIPT에서 관측 가능한 TMR 효과를 얻기 위한 일반적인 probe 사이의 거리는 10~100$\mu$m사이이다. Figure 4.12는 CIPT와 standard(patterned device) 접근법에서 각각 얻어낸 TMR measurement의 예를 결과를 보여준다.
'Magnetotransport' 카테고리의 다른 글
| Physics Origin of Universal Unusual Magnetoresistance (0) | 2025.07.15 |
|---|---|
| The Rashba Effect (0) | 2024.03.06 |
| Magnetotransport Part 2. Hall Effects (1) | 2023.12.06 |


댓글