참조 문헌
- Spin and Charge Tunneling Transport in Magnetic Tunnel Junctions With Embedded Nanoparticles
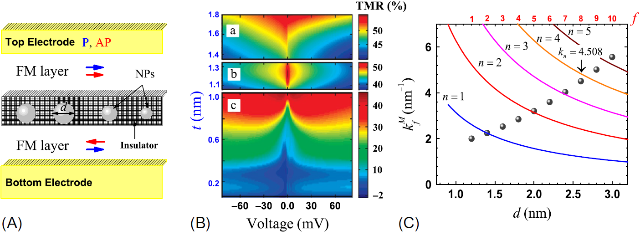
In this review we show how quasiclassical theory for point-like contacts can be adapted for spintronic device physics explaining mean free path and GMR effects in nano-scale heterocontacts, asymmetric voltage dependences of TMR in MTJs, as well as applied to modeling of zero bias TMR anomalies in MTJs with embedded nanoparticles (NPs). The dependence of in-plane component of STT on the applied voltage for various size of NPs in the case of the different barrier asymmetry can be also calculated.
GMR을 학습함에 있어, current-in-plane(CIP) GMR과 current-perpendicular-to-plane(CPP) GMR을 구분하는 것이 좋다. 이 두 타입의 GMR에 대한 물리는 상당히 다르다.
CIP GMR에서, 전자는 layer의 plane을 따라 움직이며, 그러므로 spin-dependent channeling이 다층박막의 CIP 저항을 결정하는데 중요한 역할을 한다. 그러므로 spin channel의 electronic band structure를 맞추는 것이 CIP GMR을 결정하는데, (물론 CPP GMR을 결정하는데도) 중요한 역할을 한다. 예를 들어, CIP GMR이 처음 발견된 것은 Fe-Cr 다층박막이었다. 여기서 Fe와 Cr이 매우 유사한 minority spin band를 가짐과 동시에, majority spin band는 상당히 다른 것이 발견됐다. An important implementation of spin valves used in magnetic field sensors is based on layers of Cu and Co, or materials similar to Co, in the majority channel.
CPP GMR에서 전자는 자화 층의 수직한 방향으로 움직인다. 이는 정성적으로 봤을 때 상대적으로 쉬운데, 만약 두 강자성체 레이어의 majority band, 또는 minority band가 space layer와 match할때, 스핀 채널중 하나에 ㅅㄱ하는 전자들은 magnetic moments가 align할때 잘 통과하게 된다. + vice versa.
Furthermore, some magnetic alloys, for example, Ni alloys containing Co and Fe, conduct spinup electrons with very little scattering while the spin-down electrons can hardly travel more than interatomic distance before they scatter [1]. CPP GMR is difficult to measure because the resistance of a thin film (a few nanometers) across its thickness is usually very tiny. The thickness must remain small compared with the distance over which the electrons conserve their spin projection, and which is of the order of dozen nanometers for magnetic materials. For this reason, the first CPP-GMR measurements were performed using superconducting leads.
TMR은 기하학적으로 CPP GMR과 유사한 형태를 띄며, 섹션 11.3.에서 더 자세히 다룰 예정이다. 차이점이라 하면, 비자성 금속 spacer layer가 insulator, 또는 반도체로 대체된다는 것이다. 명백하게, spin channel과 spacer layer사이의 밴드 매칭(CPP GMR의 근원)은 발생하지 않으며, 이는 insulator에ㅅ는 Fermi energy 부근에서 conduction band가 존재하지 않기 떄문이다. 이러한 이유로, TMR의 original theory는 강자성체 electrods의 Fermy energy DOS를 기반으로 하고 있다. 이 경우, GMR과는 다른 종류의 band matching이 발생하는데, 이는 매우 큰 MR 차이를 발생시킨다. 섹션 11.4.에서, 우리는 STT 현상을 다룬다. 이 현상은 Slonczewski와 Berger에 의해 독립적으로 1996년에 예견됐다. GMR과 TMR은 두 강자성체 layer 사이의 전자 수송이 그들의 magnetic moments의 상대적인 alignment에 영향을 받음에 있어 서로 반대이다.
STT에서는, 강자성체 layer를 통과하는 전류는 그들의 magnetic moments의 상대적인 방향을 변화시킬 수 있다. Spin-polarized currents는 magnetic moments의 세차운동과 magnetic configuration(P, AP)의 변화를 유발하는 것이 관측됐다.
11.2. Giant Magnetoresistance in Ferromagnetic Heteronanocontacts
11.3 Tunnel Magnetoresistance in Single- and Double-Barrier MTJ
Previously, we reviewed a theory of electronic transport through a nanosized domain wall inside the contact between ferromagnetic homo- and hetero-electrodes in a point-like geometry. This theory utilizes quasiclassical equations to describe the transport phenomena in the ferromagnetic metals, and quantum-mechanical equations for modeling the electron transmission through the domain wall, which was approximated by the sloping potential.
11.4 Spin-Transfer Torque, Size Distribution, and Temperature-Related Effects in MTJs With Embedded Nanoparticles
터널링 모델에 따르면(더 자세한 내용은 Ciudad et al의 Phys. Rev. B 85 (11) (2012) 214408을 참조), tunneling conductance는 세 항의 합으로 이루어진다.

여기서 $\alpha +\beta = 1$ 이며, $\sigma_K$는 NP를 통과하는 conductance이며 Kondo behavior에 대한 정보를 담고 있다. $\sigma_D$는 dielectric barrier를 통과하는, electrode 사이의 direc tunneling이며, $\sigma_E$는 spin flips없이 NP를 통과하는 elastic conductance이다.
The relative weight for $\alpha$ and $\beta$ depends on the fractional population of clusters on one hand, and temperature on the other.
The relationship between $\alpha$ and $\beta$ changes also with the nominal
$\mathrm{FM}^M$ thickness: it assumes $\alpha > \beta $ for thin layers since very few clusters are within the barrier,
and direct tunneling between electrodes through the barrier dielectric dominates.
When the intermediate $\mathrm{FM}^M$ layer thickness increases, it may become $ \beta > \alpha $ since number and size of the clusters increase thus increasing the contribution of the current through NPs against the direct tunneling.
$\sigma_E$와 $\sigma_K$ 사이의 관계, 그리고 결과적으로 나타나는 TMR은 layer들의 두께와 온도에 의존한다. 만약 $\sigma_K$가 우세하면, TMR은 감소하며, 반대로 $\sigma_E$가 우세하면, 낮은 온도에서 TMR은 cotunneling에 의해개선된다. The transitions are smooth, and crossover of the regimes, if any, depends on the sample design and temperature.
'MTJ' 카테고리의 다른 글
| Partial Switching (0) | 2024.03.21 |
|---|---|
| Simulated Annealing (SA) (0) | 2024.01.08 |
| 자기저항 센서 (0) | 2024.01.03 |
| Boltzmann Machine (0) | 2023.11.13 |
| Spin-Torque Diode Effect (0) | 2023.09.19 |




댓글